Bài 4: Tính chất ba đường trung tuyến của tam giác
Các câu hỏi tương tự
Cho tam giác ABC với ba trung tuyến AM,BN,CP và trọng tâm G. Chứng minh rằng:
a) \(AM< \frac{1}{2}\left(AB+AC\right)\)
b) \(\frac{3}{4}\left(AB+BC+CA\right)< AM+BN+CP< AB+BC+AC\)
Cho tam giác ABC có AB = a, AC = b, BC = c. Các trung tuyến AM, BN, CM. Chứng minh rằng :
a) BN + CP > 3a/2
b) 1/2(b-c) < AM < 1/2(b+c)
c) 3/4(a+b+c) < AM+BN+CP < a+b+c
Cho ∆ABC cân ở A, AB=34cm, BC=33cm và 3 trung tuyến AM, BN, CP đồng quy tại trọng lượng G.
a) Chứng minh AM vuông góc với BC
b) Tính độ dài AM, BN, CP. (Làm tròn kết quả đến chữ số thập phân thứ hai).
Cho tam giác ABC , đường trung tuyến AM , BN , CP . Chứng minh BN + CP > 3/2 BC
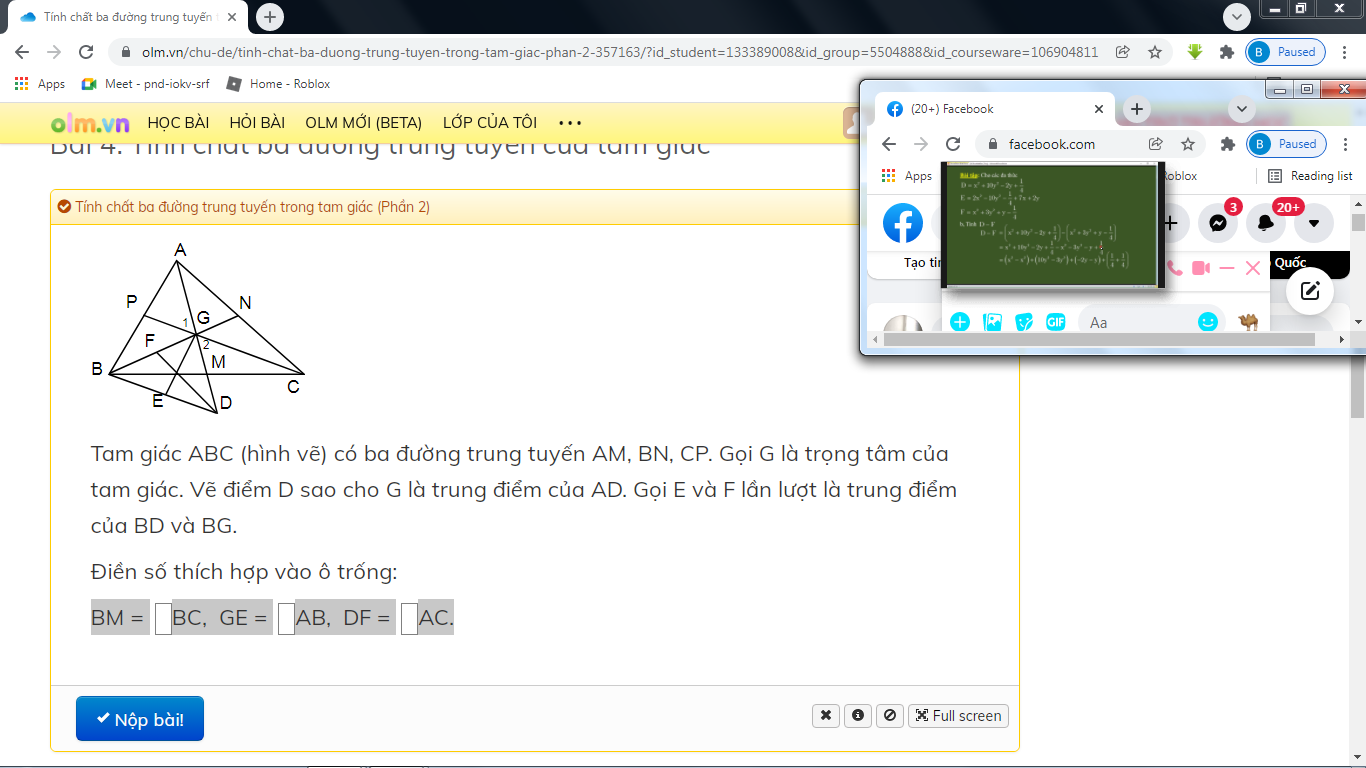
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BM =....BC, GE =.....AB, DF =........AC
Cho tam giác ABC đều, gọi G là trọng tâm của tam giác ABC
a, Chứng minh rằng: GA=GB=GC
b, Gọi AM, BN, CP lần lượt là các đường trung tuyến của tam giác. CMR: PN song song BC; MN song song AB; MP song song AC
c, CMR: tam giác PMN đều
mọi người giúp e vs ạ. e cảm ơn nhiều.
Bài 12: Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM ( M thuộc BC ). Qua M kẻ đường thẳng song song với AB , cắt AC tại N . Gọi O là giao điểm của AM và BN . Chứng minh O là trọng tam của tam giác ABC.
\(\Delta\) ABC có đường trung tuyến BN, CP; G là trọng tâm. CM: BN + CP > \(\frac{3}{2}\) BC.
1. Cho tam giác ABC, trung tuyến AM,BN,CE. CMR: AM+BN+CE<AB+AC+BC











