Rất dễ dàng tính toán \(I\left(\dfrac{a}{2};\dfrac{b}{2};\dfrac{c}{2}\right)\)
\(x_I+y_I+z_I=\dfrac{a+b+c}{2}=2\) nên I thuộc mp có pt:
\(x+y+z=2\Leftrightarrow x+y+z-2=0\)
\(d\left(M;\left(P\right)\right)=\dfrac{\left|1+2+3-2\right|}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}\)
Do \(b>1\) nên hàm \(log_bx\) đồng biến
Ta có: \(\left(a^2-25\right)^2\ge0\) ; \(\forall a\Leftrightarrow a^4-50a^2+625\ge0\Leftrightarrow a^4-25a^2+625\ge25a^2\)
\(\Rightarrow P=log_{5a}b+log_b\left(a^4-25a^2+625\right)\ge log_{5a}b+log_b\left(25a^2\right)\)
\(\Rightarrow P\ge2\sqrt{log_{5a}b.log_b\left(25a^2\right)}=2\sqrt{\dfrac{log_b\left(5a\right)^2}{log_b\left(5a\right)}}=2\sqrt{\dfrac{2log_b\left(5a\right)}{log_b5a}}=2\sqrt{2}\)
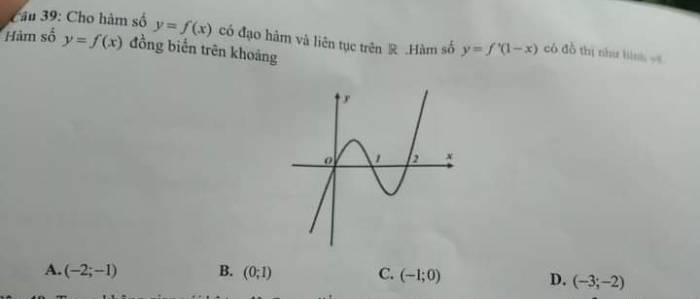
Có mấy hình vuông ạ
