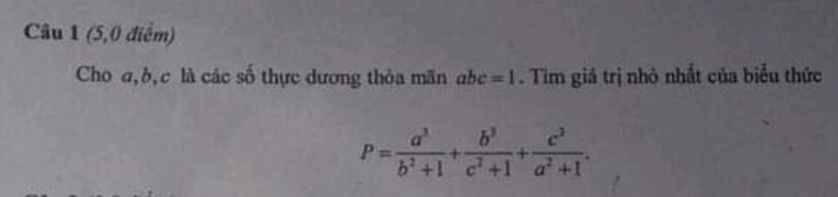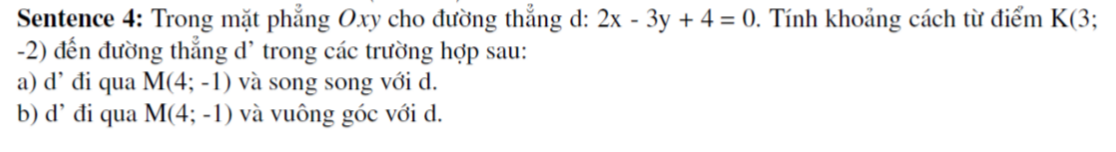Ta sẽ chứng minh \(P\ge\dfrac{3}{2}\)
\(P=\dfrac{a^4}{ab^2+a}+\dfrac{b^4}{bc^2+b}+\dfrac{c^4}{ca^2+a}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{ab^2+bc^2+ca^2+a+b+c}\)
Nên ta chỉ cần chứng minh:
\(2\left(a^2+b^2+c^2\right)^2\ge3\left(ab^2+bc^2+ca^2\right)+3\left(a+b+c\right)\)
Ta có:
\(\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{9}\left(a+b+c\right)^4\ge\dfrac{1}{9}\left(a+b+c\right).27abc=3\left(a+b+c\right)\)
Lại có:
\(ab^2+bc^2+ca^2\le\sqrt{\left(a^2b^2+b^2c^2+c^2a^2\right)\left(b^2+c^2+a^2\right)}\le\sqrt{\dfrac{1}{3}\left(a^2+b^2+c^2\right)^3}\)
Nên ta chỉ cần chứng minh:
\(\left(a^2+b^2+c^2\right)^2\ge3\sqrt{\dfrac{1}{3}\left(a^2+b^2+c^2\right)^3}\)
\(\Leftrightarrow a^2+b^2+c^2\ge3\)
Hiển nhiên đúng theo AM-GM 3 số