Đường thẳng d nhận \(\left(2;-3\right)\) là 1 vtpt
a. Đường thẳng d' song song d nên nhận \(\left(2;-3\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-4\right)-3\left(y+1\right)=0\Leftrightarrow2x-3y-11=0\)
Khoảng cách từ K đến d':
\(d\left(K;d'\right)=\dfrac{\left|2.3-3.\left(-2\right)-11\right|}{\sqrt{2^2+\left(-3\right)^2}}=...\) bạn tự bấm máy
b. Do d' vuông góc d nên nhận \(\left(3;2\right)\) là 1 vtpt
Phương trình d':
\(3\left(x-4\right)+2\left(y+1\right)=0\Leftrightarrow3x+2y-10=0\)
Khoảng cách:
\(d\left(K;d'\right)=\dfrac{\left|3.3+2.\left(-2\right)-10\right|}{\sqrt{3^2+2^2}}=...\)

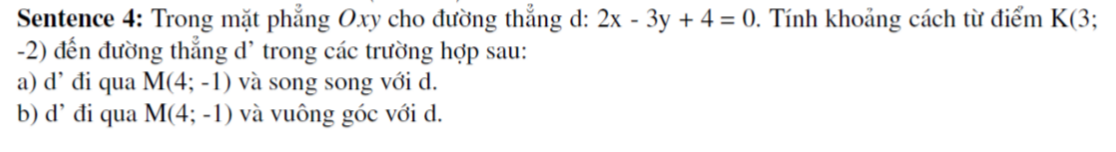




















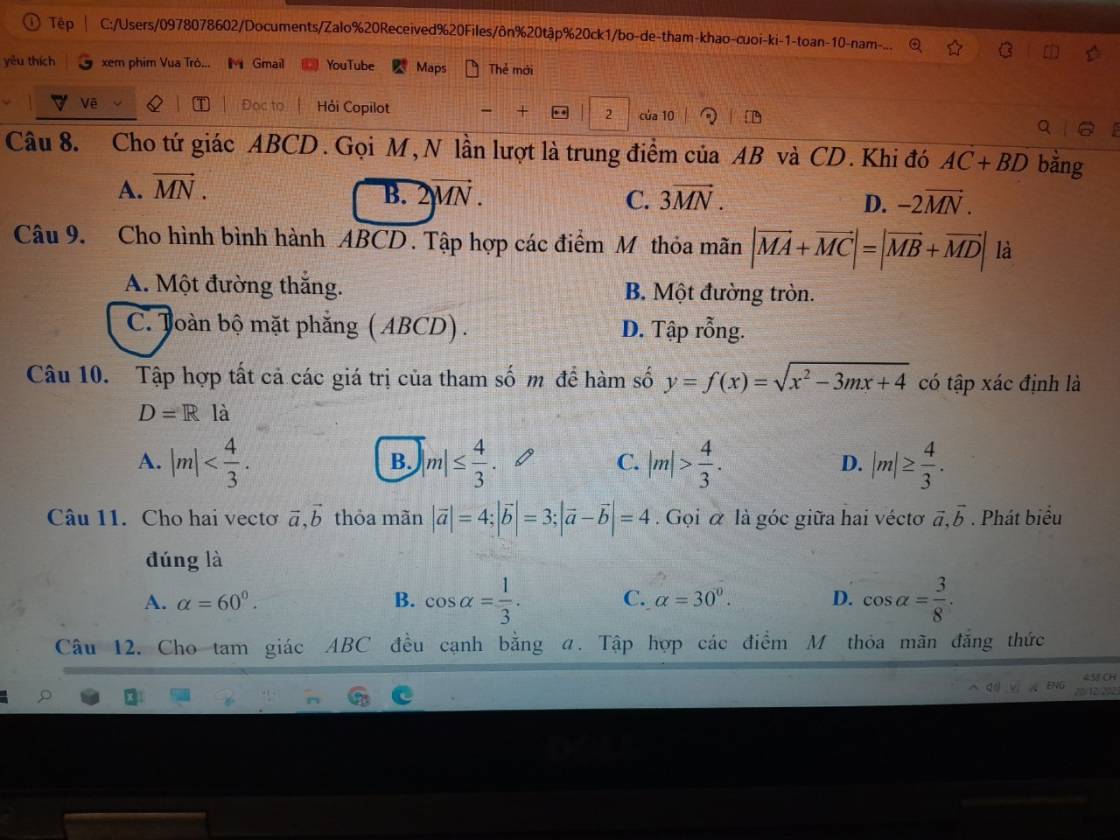 giúp tớ câu 9 với ạ
giúp tớ câu 9 với ạ