12.1
Giả sử \(G=\left(m;2m-2\right)\left(m\in R\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_H=2x_E-x_G=6-m\\y_H=2y_E-y_G=2-2m\end{matrix}\right.\)
\(\Rightarrow H=\left(6-m;2-2m\right)\)
Mà \(H\in d_2\Rightarrow6-m+2-2m+3=0\Leftrightarrow m=\dfrac{11}{3}\)
\(\Rightarrow G=\left(\dfrac{11}{3};\dfrac{16}{3}\right)\)
\(\Rightarrow\Delta:8x-y-24=0\)
12.2
Giả sử \(A=\left(m;-m-1\right)\left(m\in R\right)\)
Ta có: \(\vec{AM}=\dfrac{1}{3}\vec{MB}\)
\(\Rightarrow\left\{{}\begin{matrix}x_M-x_A=\dfrac{1}{3}\left(x_B-x_M\right)\\y_M-y_A=\dfrac{1}{3}\left(y_B-y_M\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-m=\dfrac{1}{3}\left(x_B-1\right)\\m+1=\dfrac{1}{3}.y_B\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B=4-3m\\y_B=3m+3\end{matrix}\right.\)
\(\Rightarrow B=\left(4-3m;3m+3\right)\)
Mà \(B\in d_2\Rightarrow4-3m-2\left(3m+3\right)+2=0\Leftrightarrow m=0\)
\(\Rightarrow A=\left(0;-1\right)\)
\(\Rightarrow d:x-y-1=0\)














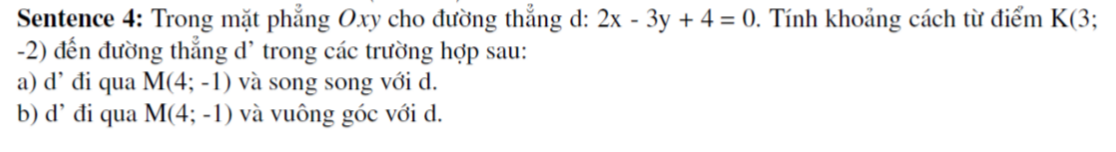

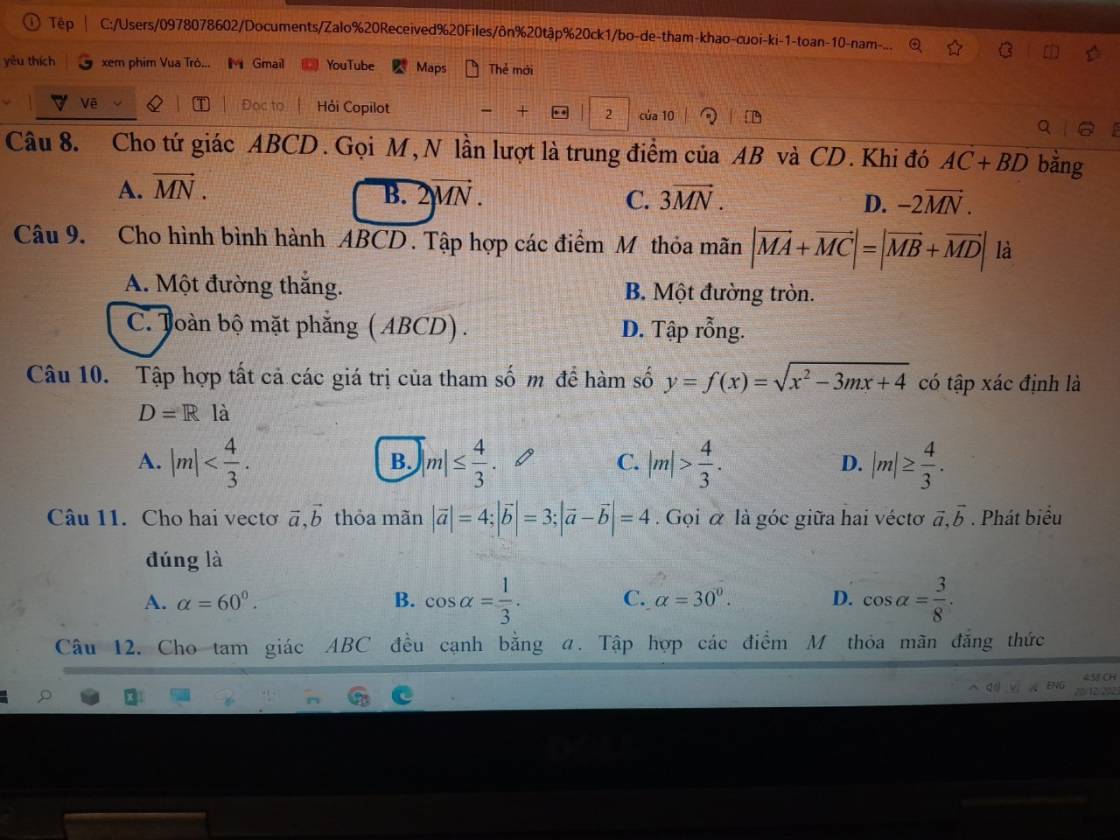 giúp tớ câu 9 với ạ
giúp tớ câu 9 với ạ





