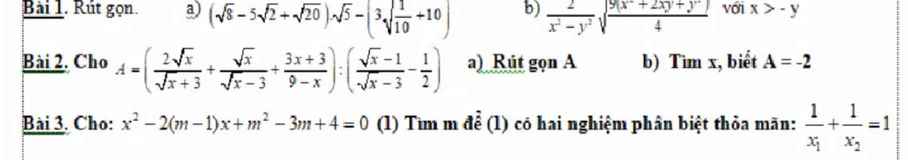e) Vì pt luôn có nghiệm với mọi m , theo vi-ét ta có :
\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m+2\end{matrix}\right.\dfrac{\left(1\right)}{\left(2\right)}\)
Giả sử \(x_1=2x_2\) \(\left(3\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có hpt :
\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1=2x_2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x_2=m+3\\x_1=2x_2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+3}{3}\\x_1=2x_2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+3}{3}\\x_1=\dfrac{2m+6}{3}\end{matrix}\right.\)
Thay \(x_1=\dfrac{2m+6}{3}\) và \(x_2=\dfrac{m+3}{3}\) vào \(\left(2\right)\) ta có :
\(x_1\cdot x_2=m+2\)
\(\Leftrightarrow\dfrac{2m+6}{3}\cdot\dfrac{m+3}{3}=m+2\\ \Leftrightarrow\left(2m+6\right)\left(m+3\right)=9\left(m+2\right)\\ \Leftrightarrow2\left(m+3\right)\left(m+3\right)=9m+18\)
\(\Leftrightarrow2\left(m^2+6m+9\right)=9m+18\\ \Leftrightarrow2m^2+12m+18=9m+18\)
\(\Leftrightarrow2m^2+3m=0\)
\(\Leftrightarrow m\left(2m+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}m=0\\2m+3=0\end{matrix}\right.\\ \left[{}\begin{matrix}m=0\\m=-\dfrac{3}{2}\end{matrix}\right.\)





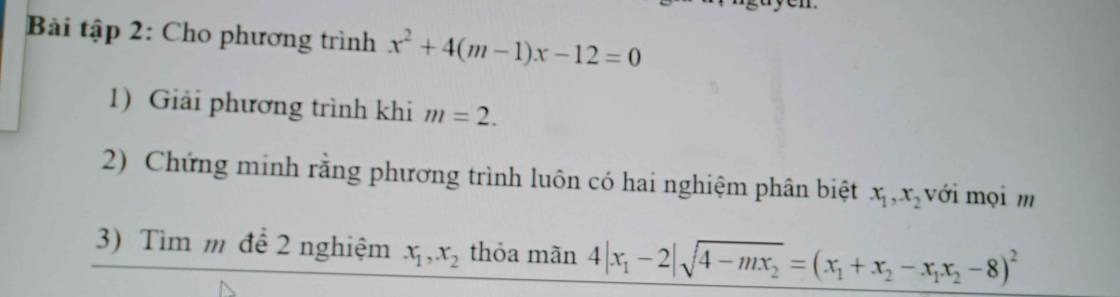


 e b
e b