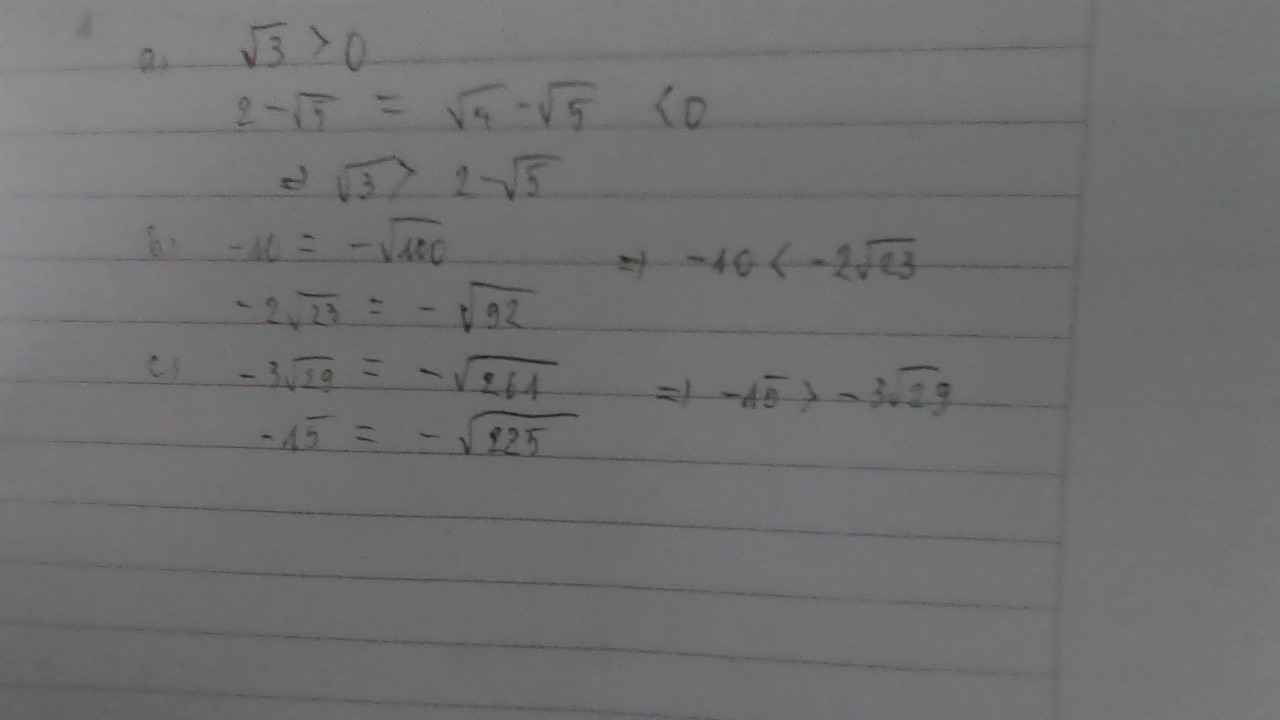Bài 1: Căn bậc hai
Các câu hỏi tương tự
bài 1: tìm điều kiện xác định với giá trị nào của x thì các biểu thức sau đây xác định
a, \(\sqrt{-2x+3}\)
b, \(\sqrt{3x+4}\)
c, \(\sqrt{1+x\overset{2}{ }}\)
d, \(\sqrt{^{-3}_{3x+5}}\)
e, \(\sqrt{\dfrac{2}{x}}\)
help me :((
1. Rút gọn \(A=\sqrt{x+\sqrt{2x-1}}-\sqrt{x-\sqrt{2x-1}}\)
2. Tính \(B=\frac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{\sqrt{5}+1}}-\sqrt{3-2\sqrt{2}}\)
3.Tính \(C=\frac{\sqrt{3-\sqrt{5}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\cdot\left(3+\sqrt{5}\right)}{\left(4+\sqrt{15}\right)\cdot\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}}\)
1) sqrt{x-1}sqrt{2x+3}
2) sqrt{2x-3}sqrt{x-1}
3) sqrt{2-x}sqrt{3+x}
4) sqrt{4x-8}2sqrt{x-2}
5) sqrt{x^2-5}sqrt{4x-9}
6) sqrt{x-2}sqrt{x^2-2x}
7) sqrt{x^2-3x}sqrt{15-5x}
8) sqrt{4x^2-9}sqrt{-20-18}
Có điều kiện cho từng câu hộ mình nhé!!!
9) sqrt{x-2}sqrt{x-2}
Đọc tiếp
1) \(\sqrt{x-1}=\sqrt{2x+3}\)
2) \(\sqrt{2x-3}=\sqrt{x-1}\)
3) \(\sqrt{2-x}=\sqrt{3+x}\)
4) \(\sqrt{4x-8}=2\sqrt{x-2}\)
5) \(\sqrt{x^2-5}\sqrt{4x-9}\)
6) \(\sqrt{x-2}=\sqrt{x^2-2x}\)
7) \(\sqrt{x^2-3x}=\sqrt{15-5x}\)
8) \(\sqrt{4x^2-9}=\sqrt{-20-18}\)
Có điều kiện cho từng câu hộ mình nhé!!!
9) \(\sqrt{x-2}=\sqrt{x-2}\)
giải các pt
1, \(\sqrt{2x^2+8x+6}+\sqrt{x^2-1}=2x+2\)
2, \(\sqrt{x+2\sqrt{x-1}}-\sqrt{x-2\sqrt{x-1}}=2\)
3, \(\sqrt{x^2+x+4}+\sqrt{x^2+x+1}=\sqrt{2x^2+2x+9}\)
4, \(2x^2+\sqrt{x^2-4x+12}=4x+8\)
5, \(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\)
So sánh:a, 5+sqrt{ }2 và 4+ sqrt{ }3b, sqrt{ }8 - sqrt{ }2 và sqrt{ }5 - sqrt{ }3c, sqrt{ }5 - sqrt{ }3 và sqrt{ }10 - sqrt{ }7
Đọc tiếp
So sánh:
a, 5+\(\sqrt{ }\)2 và 4+ \(\sqrt{ }\)3
b, \(\)\(\sqrt{ }\)8 - \(\sqrt{ }\)2 và \(\sqrt{ }\)5 - \(\sqrt{ }\)3
c, \(\sqrt{ }\)5 - \(\sqrt{ }\)3 và \(\sqrt{ }\)10 - \(\sqrt{ }\)7
Bài 1:
a) sqrt{13-2sqrt{42}}
b) sqrt{46+6sqrt{5}}
c) sqrt{12-3sqrt{15}}
d) sqrt{11+sqrt{96}}
Bài 2:
a) Asqrt{6+2sqrt{2}sqrt{3-sqrt{4+2sqrt{3}}}}
b) Bsqrt{5}-sqrt{3-sqrt{29-12sqrt{5}}}
c) Csqrt{3-sqrt{5}}left(sqrt{10}+sqrt{2}right)left(3+sqrt{5}right)
d) Dsqrt{4+sqrt{7}}-sqrt{4-sqrt{7}}
e) Esqrt{8+2sqrt{10+2sqrt{5}}}+sqrt{8-2sqrt{10+2sqrt{5}}}
g) Gsqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}
h) H4x-sqrt{9x^2-12x+4}
i) frac{sqrt{7}-sqrt{2}}{sqrt{7}+sqrt{2}}+frac{sqrt{7}+sqrt{2}}{sqrt{7}-sqrt...
Đọc tiếp
Bài 1:
a) \(\sqrt{13-2\sqrt{42}}\)
b) \(\sqrt{46+6\sqrt{5}}\)
c) \(\sqrt{12-3\sqrt{15}}\)
d) \(\sqrt{11+\sqrt{96}}\)
Bài 2:
a) \(A=\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{4+2\sqrt{3}}}}\)
b) \(B=\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}\)
c) \(C=\sqrt{3-\sqrt{5}}\left(\sqrt{10}+\sqrt{2}\right)\left(3+\sqrt{5}\right)\)
d) \(D=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
e) \(E=\sqrt{8+2\sqrt{10+2\sqrt{5}}}+\sqrt{8-2\sqrt{10+2\sqrt{5}}}\)
g) \(G=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
h) \(H=4x-\sqrt{9x^2-12x+4}\)
i) \(\frac{\sqrt{7}-\sqrt{2}}{\sqrt{7}+\sqrt{2}}+\frac{\sqrt{7}+\sqrt{2}}{\sqrt{7}-\sqrt{2}}\)
Rút gọn các biểu thức saua,Aleft(dfrac{1}{x-sqrt{x}}+dfrac{1}{sqrt{x}-1}right):dfrac{sqrt{x}+1}{x-2sqrt{x}+1}b,Bdfrac{2sqrt{x}-1}{sqrt{x}+1}+dfrac{3sqrt{x}-1}{x-sqrt{x}+1}-dfrac{2xsqrt{x}-2x+2sqrt{x}-3}{xsqrt{x}+1}c,Cleft(1-dfrac{x+3sqrt{x}}{x-9}right):left(dfrac{sqrt{x}-3}{2-sqrt{x}}+dfrac{sqrt{x}-2}{3+sqrt{x}}-dfrac{9-x}{x+sqrt{x}-6}right)d,Dleft(dfrac{sqrt{x}}{3+sqrt{x}}+dfrac{x+9}{9-x}right):left(dfrac{3sqrt{x}+1}{x-3sqrt{x}}-dfrac{1}{sqrt{x}}right)e,Edfrac{15sqrt{x}-11}{x+2sqrt{x}-3}+dfrac{...
Đọc tiếp
Rút gọn các biểu thức sau
a,\(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)
b,\(B=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{3\sqrt{x}-1}{x-\sqrt{x}+1}-\dfrac{2x\sqrt{x}-2x+2\sqrt{x}-3}{x\sqrt{x}+1}\)
c,\(C=\left(1-\dfrac{x+3\sqrt{x}}{x-9}\right):\left(\dfrac{\sqrt{x}-3}{2-\sqrt{x}}+\dfrac{\sqrt{x}-2}{3+\sqrt{x}}-\dfrac{9-x}{x+\sqrt{x}-6}\right)\)
d,\(D=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
e,\(E=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
Giải các phương trình vô tỉ (Phương trình có chứa căn thức)
1) sqrt{x^2-20x+100}10
2) sqrt{x+2sqrt{x}+1}6
3) sqrt{x^2-6x+9}sqrt{4+2sqrt{3}}
4) sqrt{3x+2sqrt{3x}+1}5
5) sqrt{x^2+2xsqrt{3}+3}sqrt{4-2sqrt{3}}
6) sqrt{6x+4sqrt{6x}+4}7
7) sqrt{2x^2-2xsqrt{6}+3}-sqrt{5-sqrt{24}}0
8) sqrt{3-2sqrt{2}}-sqrt{x^2-2xsqrt{2}+2}0
9) sqrt{11-sqrt{120}}sqrt{5x^2+xsqrt{120}+6}
Đọc tiếp
Giải các phương trình vô tỉ (Phương trình có chứa căn thức)
1) \(\sqrt{x^2-20x+100}=10\)
2) \(\sqrt{x+2\sqrt{x}+1}=6\)
3) \(\sqrt{x^2-6x+9}=\sqrt{4+2\sqrt{3}}\)
4) \(\sqrt{3x+2\sqrt{3x}+1}=5\)
5) \(\sqrt{x^2+2x\sqrt{3}+3}=\sqrt{4-2\sqrt{3}}\)
6) \(\sqrt{6x+4\sqrt{6x}+4}=7\)
7) \(\sqrt{2x^2-2x\sqrt{6}+3}-\sqrt{5-\sqrt{24}}=0\)
8) \(\sqrt{3-2\sqrt{2}}-\sqrt{x^2-2x\sqrt{2}+2}=0\)
9) \(\sqrt{11-\sqrt{120}}=\sqrt{5x^2+x\sqrt{120}+6}\)
giải các phương trình sau:
\(\)1, \(\sqrt{10-x}+\sqrt{x+3}\)=5
2, \(\sqrt{15-x}+\sqrt{3-x}\)=6
3, \(\sqrt{4x+1}-\sqrt{3x+4}=1\)
4, \(\sqrt{x+\sqrt{2x-1}}\)+\(\sqrt{x-\sqrt{2x-1}}=\sqrt{2}\)
5, \(\sqrt{x^2-4x+4}+\sqrt{x^2-6x+9}=1\)
Giải các pt sau:
1, \(\sqrt{x^2+x+1}=2x+\sqrt{x^2-x+1}\)
2, \(2x^2+2x+6=2x\sqrt{x^2-x+1}+4\sqrt{3x+1}\)
3, \(\left(\sqrt{x+3}-\sqrt{x}\right)\left(1+\sqrt{x^2+3x}\right)=3\)
4, \(\sqrt{2x^2-1}+\sqrt{x^2-3x-2}=\sqrt{2x^2-2x+3}+\sqrt{x^2-x+2}\)
5, \(13\sqrt{x-1}+9\sqrt{x+1}=16x\)