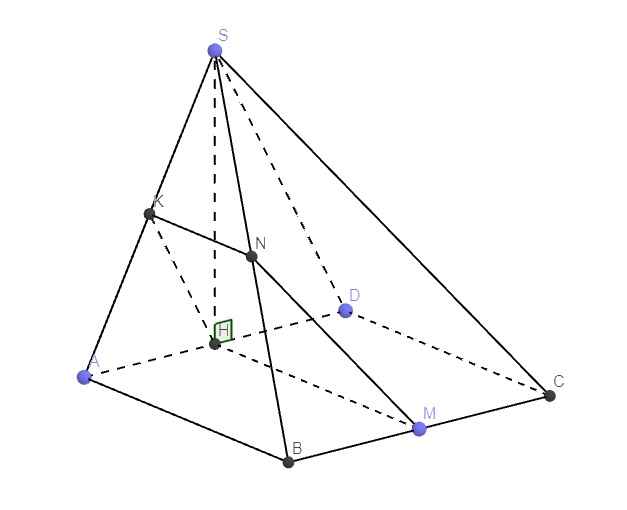
Bài 1 : cho hình chóp SABCD có đáy ABCD là hình vuông và SH vuông góc với mặt phẳng ( ABCD ) tại trung điểm H của cạnh AD .
a, CM tam giác SCD vuông
b, Gọi M,K là trung điểm BC , SA . Chứng minh ( SCD ) song song ( HKM )
c, ( HKM ) cắt SB tại N . Chứng minh HKMN là hình thang vuông
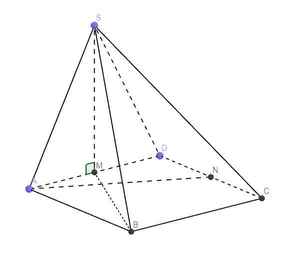
Bài 2 : cho hình chóp SABCD đáy là hình vuông và SM vuông với ( ABCD ) với M là trung điểm AD .
a, CM : tam giác SAB và tam giác SCD vuông
b, Gọi N là trung điểm CD , CM AN vuông góc với ( SMB)
giúp mình với nha , cảm ơn nhiều ạ
1.
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
b.
Do H là trung điểm AD, K là trung điểm SA
\(\Rightarrow KH\) là đường trung bình tam giác SAD
\(\Rightarrow KH||SD\Rightarrow KH||\left(SCD\right)\)
H là trung điểm AD, M là trung điểm BC \(\Rightarrow HM||CD\)
\(\Rightarrow HM||\left(SCD\right)\)
Mà HM cắt KH tại H
\(\Rightarrow\left(HKM\right)||\left(SCD\right)\)
c.
Qua K kẻ đường thẳng song song AB cắt SB tại N
\(\Rightarrow N=\left(HKM\right)\cap SB\)
\(\left\{{}\begin{matrix}KN||AB\\HM||AB\end{matrix}\right.\) \(\Rightarrow KN||HM\) (1)
Mặt khác \(\left\{{}\begin{matrix}HM||CD\\CD||\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM\perp KH\) (2)
(1);(2) \(\Rightarrow\) HKNM là hình thang vuông
2.
a.
Ta có: \(\left\{{}\begin{matrix}SM\perp\left(ABCD\right)\Rightarrow SM\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow AB\perp SA\)
\(\Rightarrow\Delta SAB\) vuông tại A
Lại có \(\left\{{}\begin{matrix}CD||AB\\AB\perp\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
b.
Ta có: \(\overrightarrow{AN}.\overrightarrow{BM}=\left(\overrightarrow{AD}+\overrightarrow{DN}\right)\left(\overrightarrow{BA}+\overrightarrow{AM}\right)=\left(\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)\left(-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)\)
\(=-\overrightarrow{AD}.\overrightarrow{AB}+\dfrac{1}{2}AD^2-\dfrac{1}{2}AB^2+\dfrac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}=0\)
\(\Rightarrow AN\perp BM\) (1)
Mà \(SM\perp\left(ABCD\right)\Rightarrow SM\perp AN\) (2)
(1);(2) \(\Rightarrow AN\perp\left(SMB\right)\)