Bài 7: Định lí
Các câu hỏi tương tự
Cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc BAE
MN làm giúp em trước 15:45, em cảm ơn ạ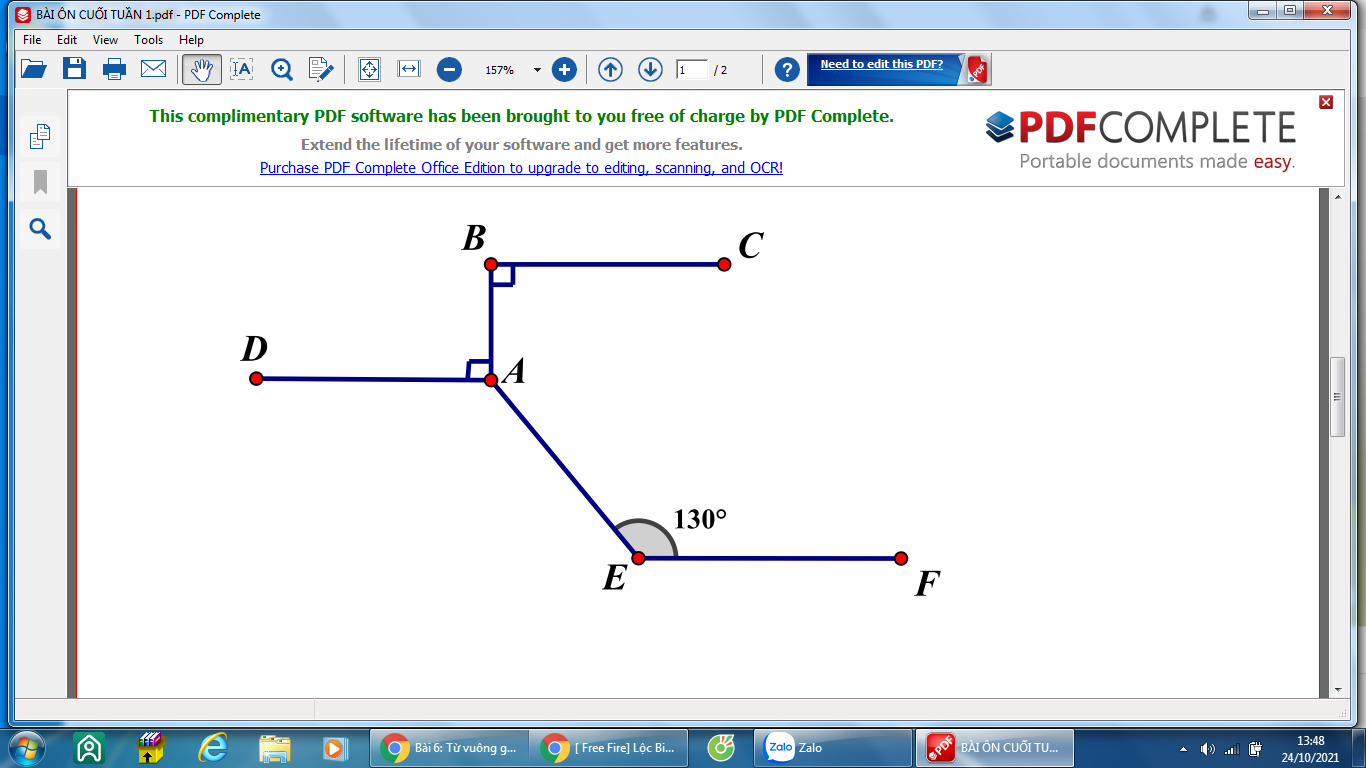
Chứng minh rằng :a) Nếu 2 góc xOy và góc xOy cùng nhọn hoặc cùng tù có Ox vuông góc với Ox và Oy vuông góc với Oy thì góc xOy góc xOy b) Nếu góc xOy nhọn; góc xOy tù và có Ox vuông góc với Ox Oy vuông góc với Oy thì góc xOy + góc xOy 180 độ
Đọc tiếp
Chứng minh rằng :
a) Nếu 2 góc xOy và góc x'O'y' cùng nhọn hoặc cùng tù có Ox vuông góc với Ox' và Oy vuông góc với Oy' thì góc xOy = góc x'O'y'
b) Nếu góc xOy nhọn; góc x'O'y' tù và có Ox vuông góc với Ox' Oy vuông góc với Oy' thì góc xOy + góc x'O'y' =180 độ
Bài 1: Cho ∆ABC vuông tại B. Tia phân giác góc A cắt cạnh BC tại D. Trên tia AC lấy điểm H sao cho AH=AB a) Chứng minh: ∆ABD = ∆AHD. b) Chứng minh: DH vuông góc với AC
Chứng minh rằng
a) Nếu 2 góc xOy và góc x'O'y' cùng nhọn hoặc cùng tù có Ox vuông góc với Ox' và Oy vuông góc với Oy' thì góc xOy = góc x'O'y' b) Nếu góc xOy nhọn; góc x'O'y' tù và có Ox vuông góc với Ox' Oy vuông góc với Oy' thì góc xOy + góc x'O'y' = 180 độ
Cho định lý : nếu 1 đường thẳng cách 2 đuờng thẳng và trong các góc tạo thành có 1 cặp góc sole trong bằng nhau thì 2 góc trong cùng phía bù nhau Vẽ hình, giả thiết, kết luận, chứng minh
Cho định lí : Nếu hai đường thẳng xx, yy cắt nhau tại O và góc xOy vuông thì các góc yOx, xOy, yOx đều là góc vuông
a) Hãy vẽ hình
b) Viết giả thiết và kết luận của định lí
c) Điền vào chỗ trống (.......) trong các câu sau :
d) Hãy trình bày lại chứng minh một cách thu gọn hơn
Đọc tiếp
Cho định lí : "Nếu hai đường thẳng xx', yy cắt nhau tại O và góc xOy vuông thì các góc yOx', x'Oy', y'Ox đều là góc vuông"
a) Hãy vẽ hình
b) Viết giả thiết và kết luận của định lí
c) Điền vào chỗ trống (.......) trong các câu sau :

d) Hãy trình bày lại chứng minh một cách thu gọn hơn
cho góc nhọn xOy.trên hai canh OX và OY lần lượt lấy hai điểm A và B sao cho OA =OB.tia phân giác của góc XOY cắt ab tại I.
a/ chứng minh: oi là đường trung trực của AB
b/ Kẻ AD vuông góc với Oy (D thuộc Oy);C là giao điểm của AD với OI .Chứng minh BC vuông góc với Ox.
c/BC cắt Ox tại E. C hứng minh :DE song song với AB
Bài 2: Cho góc xOy khác góc bẹt. Trên tia Ox lấy điểm M, trên tia Oy lấy điểm N sao cho OM = ON. Đoạn thẳng MN cắt tia Oz là tia phân giác của góc xOy tại điểm P. Chứng minh: a) ∆MOP = ∆NOP. b) P là trung điểm của MN. c) OP vuông góc với MN.
Cho tam giác abc có 3 góc nhọn , kẻ ah vuông góc bc tại h , bít hc nhỏ hơn hb. Chứng minh ac nhỏ hơn ab
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng. b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
Đọc tiếp
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.
a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng.
b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.











