Bài 7: Định lí
Các câu hỏi tương tự
Cho gọc xOy,lấy điểm a,b thuộc tia Ox, lấy điểm c,d thuộc tia Ox sao cho OA=OC;OD=OB.Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD=BC
b) Tam giác EAB= Tam giác ECD
c)OE là phân giác của xOy
Mọi người giúp mình với ạ. Vẽ hình nữa nhé mọi người. Cảm ơn m.n rất nhiều :3
Trên hình vẽ cho biết : NM_x'=130º, MN_P=80º và NP_y=30º. Chứng minh xx'//yy'. Cảm ơn ạ , mìk đag cần gấp
cho góc nhọn xOy.trên hai canh OX và OY lần lượt lấy hai điểm A và B sao cho OA =OB.tia phân giác của góc XOY cắt ab tại I.
a/ chứng minh: oi là đường trung trực của AB
b/ Kẻ AD vuông góc với Oy (D thuộc Oy);C là giao điểm của AD với OI .Chứng minh BC vuông góc với Ox.
c/BC cắt Ox tại E. C hứng minh :DE song song với AB
Vẽ hình, ghi giả thiết kết luận và chứng minh định lí : “Nếu hai đường thẳng song song thì các tia phân giác của mỗi cặp góc đồng vị song song với nhau.”
làm giúp mk nha
giúp mình câu b với d nha , câu b là tính góc k1, mình cảm ơn 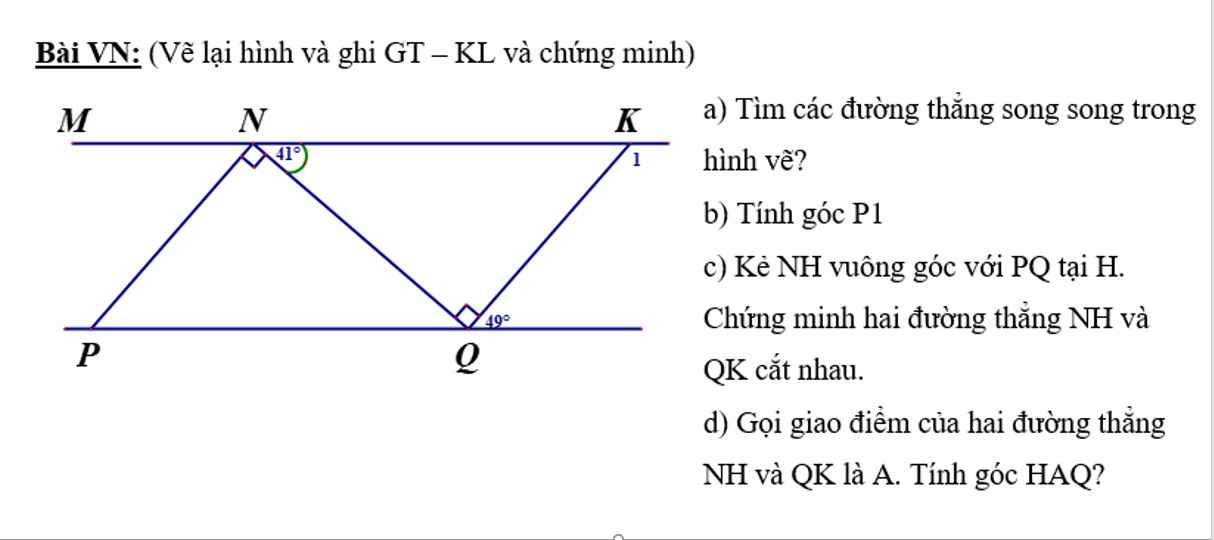
Bài 1. Cho tam giác ABC, biết : AB 3cm,AC 4cm,BC 5cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD 6cm. Tính độ đài đoạn thẳng BD.
Bài 2. Cho tam giác ABC, biết AB 12cm,AC 9cm,BC15cm.
a) Chứng tỏ tam giác ABC vuông .
b) Kẻ AH vuông góc với BC tại H, biết AH 7,2 cm. Tính độ đài đoạn thẳng BH và
HC.
Bài 3.Cho tam giác nhọn ABC (AB AC). Kẻ AH vuông góc với BC tại H. Tính chu
vi tam giác ABC biết
AC20cm, AH 12cm, BH 5cm .
Bài 4. Cho tam giác ABC cân t...
Đọc tiếp
Bài 1. Cho tam giác ABC, biết : AB =3cm,AC= 4cm,BC= 5cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD = 6cm. Tính độ đài đoạn thẳng BD.
Bài 2. Cho tam giác ABC, biết AB =12cm,AC= 9cm,BC=15cm.
a) Chứng tỏ tam giác ABC vuông .
b) Kẻ AH vuông góc với BC tại H, biết AH = 7,2 cm. Tính độ đài đoạn thẳng BH và
HC.
Bài 3.Cho tam giác nhọn ABC (AB < AC). Kẻ AH vuông góc với BC tại H. Tính chu
vi tam giác ABC biết
AC=20cm, AH =12cm, BH =5cm .
Bài 4. Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC
a) Chứng minh tam giác AHB= AHC và H là trung điểm của BC.
b) Từ H kẻ HM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho
BM =CN .Chứng minh HN vuông góc AC .
Bài 5. Cho tam giác ABC cân tại A, tia phân giác của góc A cắt BC tại I
a) Chứng minh tam giác AIB = tam giác AIC
b) Lấy M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng
minh AD // BC và AI vuông góc AD.
c) Vẽ AH vuông góc BD tại H, vẽ CK vuông góc BD tại K. Chứng minh BH = DK
Bài 6.Cho tam giác ABC vuông tại A, đường phân giác BD.Kẻ AE = BD (E thuộc BD). AE cắt BC ở K.
a) Chứng minh tam giác ABE= KBE và suy ra tam giác BAK cân.
b) Chứng minh tam giác ABD =KBD và DK vuông góc BC.
c) Kẻ AH vuông góc BC (H thuộc BC). Chứng minh AK là tia phân giác của
HAC.
Bài 1: Cho ∆ABC vuông tại B. Tia phân giác góc A cắt cạnh BC tại D. Trên tia AC lấy điểm H sao cho AH=AB a) Chứng minh: ∆ABD = ∆AHD. b) Chứng minh: DH vuông góc với AC
Ghi giả thiết, kết luận và chứng minh định lí : "Nếu hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì a và b song song với nhau"
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng. b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
Đọc tiếp
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.
a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng.
b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.