Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3km và muốn đến điểm B ở bờ đối diện cách 8km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyển thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6km/h và vận tốc chạy bộ là 8km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
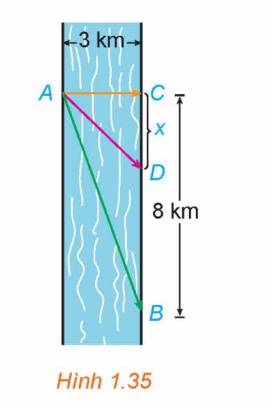
Gọi độ dài đoạn CD là x (km \(0 < x < 8\))
Quãng đường AD dài: \(\sqrt {A{C^2} + D{C^2}} = \sqrt {9 + {x^2}} \left( {km} \right)\)
Quãng đường BD dài \(8 - x\left( {km} \right)\)
Thời gian người đó đi đến B bằng cách chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B là: \(\frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) (giờ)
Xét hàm số \(y = \frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) với \(0 < x < 8\)
Ta có: \(y' = \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8}\)
\(y' = 0 \Leftrightarrow \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8} = 0 \Leftrightarrow 4x = 3\sqrt {9 + {x^2}} \Leftrightarrow \left\{ \begin{array}{l}16{x^2} = 9\left( {9 + {x^2}} \right)\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \frac{{81}}{7}\\x > 0\end{array} \right. \Leftrightarrow x = \frac{9}{{\sqrt 7 }}\)
Bảng biến thiên:
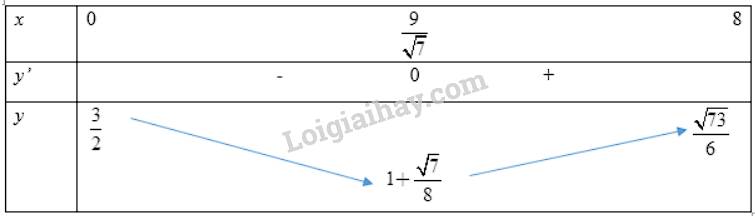
Vậy anh An phải chèo thuyền sang bờ ở điểm D cách B một khoảng bằng \(\frac{9}{{\sqrt 7 }}km\) thì đến B sớm nhất.


