Question

a) Quan sát Hình 11, chứng minh \(AK\) là đường phân giác của góc \(A\) trong tam giác \(ABC\).

b) Dựa vào kết quả của câu a, hãy nêu cách vẽ đường phân giác của một góc trong tam giác bằng thước kẻ và eke.

Answer 1

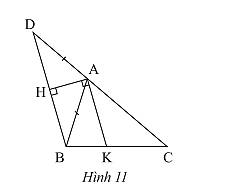
a) Vì \(\left\{ \begin{array}{l}AK \bot HA\\BD \bot HA\end{array} \right. \Rightarrow AK//BD\) (từ vuông góc đến song song)

Xét tam giác \(BCD\) có \(AK//BD\), theo định lí Thales ta có:

\(\frac{{KC}}{{KB}} = \frac{{AC}}{{AD}}\).

Mà \(AD = AB\) (gt), nên \(\frac{{KC}}{{KB}} = \frac{{AC}}{{AB}}\).

Xét tam giác \(ABC\) ta có:

\(\frac{{KC}}{{KB}} = \frac{{AC}}{{AB}} \Rightarrow AK\) là đường phân giác của góc \(A\) trong tam giác \(ABC\).

b) Vẽ đường phân giác của một góc trong tam giác bằng thước kẻ và eke.

Giả sử ta vẽ đường phân giác góc \(A\) của tam giác \(ABC\).

Bước 1: Trên tia đối của tia \(AC\) lầy điểm \(D\) sao cho \(AD = AC\);

Bước 2: Vẽ \(AH\) vuông góc với \(BD\);

Bước 3: Vẽ \(AK\) vuông góc với \(AH\) tại \(A\).

Bước 4: Khi đó, \(AK\) là đường phân giác góc \(A\) trong tam giác \(ABC\).

Answer 2

a: AK//BD(cùng vuông góc với AH)

=>góc CAK=góc D; góc BAK=góc ABD

mà góc D=góc ABD

nên góc CAK=góc BAK

=>AK là phân giác của góc BAC

b: