56\(\dfrac{1}{3}\) . \(x^2\) + 2 là đa thức bậc 2
Chương II : Hàm số và đồ thị
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
bài 1chodfrac{sqrt{x}+1}{sqrt{x}-3}tìm số nguyên x để A có giá trị là một số nguyênbài 2tìm giá trị lớn nhất của các biểu thức sauA5-(2x-1)^2 Bdfrac{1}{2cdotleft(x-1right)^2+3} Cdfrac{x^2+8}{x^2+2} Ddfrac{1}{sqrt{x}+3}bài 3 tìm các giá trị nguyên của x để biểu thức sau có giá trị nhỏ nhất Adfrac{1}{x-3} Bdfrac{7-x}{x-5} Cdfrac{5x-19}{x-4}bài 4ba số a,b,c khác 0 và a+b+cne,thỏa mãn điều kiện dfrac{a}{b+c}dfrac{b}{c+a}dfrac{c}{a+b}tính giá trị biểu thức...
Đọc tiếp
bài 1
cho\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)tìm số nguyên x để A có giá trị là một số nguyên
bài 2
tìm giá trị lớn nhất của các biểu thức sau
A=5-(2x-1)\(^2\) B=\(\dfrac{1}{2\cdot\left(x-1\right)^2+3}\) C=\(\dfrac{x^2+8}{x^2+2}\) D=\(\dfrac{1}{\sqrt{x}+3}\)
bài 3 tìm các giá trị nguyên của x để biểu thức sau có giá trị nhỏ nhất
\(A=\dfrac{1}{x-3}\) B\(=\dfrac{7-x}{x-5}\) C\(=\dfrac{5x-19}{x-4}\)
bài 4
ba số a,b,c khác 0 và a+b+c\(\ne\),thỏa mãn điều kiện \(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}\)
tính giá trị biểu thức \(P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\)
Cho hai đa thức: m = 3( xy^2z)^2 và n= (-xy)^2 xy^2z^2 a) thu gọn các đơn thức chuyên rồi cho biết bậc của đa thức m b) Tính giá trị của đa thức p + m = n và x = z = -2 y = -1
tính tích của các đơn thức sau rồi tìm Bậc của đơn thức thu được:\(\left(\dfrac{-1}{3}x^2y\right)\times\left(6xy^2\right)\)
Cho đa thức f(x) thỏa mãn các điều Kiện sau
+)f(x) là đa thức bậc 2
+) f(0)=1
+) f(x) có một nghiệm là x=1 và 1 nghiệm x=-1
a) Tìm đa thức f(x)
b) tìm GTLN của đa thức f(x)
Cho đa thức a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến. b) Tìm bậc và các hệ số của Q(x). c) Chứng tỏ Q(x) không có nghiệm.
Đọc tiếp
Cho đa thức 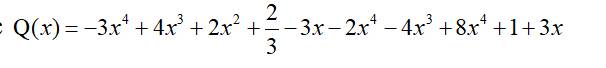
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
b) Tìm bậc và các hệ số của Q(x).
c) Chứng tỏ Q(x) không có nghiệm.
1/ Cho hai đa thức f(x) = 5x - 7 và g(x) = 3x + 1
a) Tìm nghiệm của hai đa thức trên
b) Tính h(x) = f(x) - g(x) và tìm nghiệm của h(x)
2/ Cho f(x) = x2 + 4x - 5
a) Số -5 có phải là nghiệm của f(x) không?
b) Tính g(x) biết g(x) - f(x) = 2x + 7
1. Chứng tỏ các đa thức sau ko có nghiệm
a, x2 + 3 b, ( x - 5 )2 +1
2.Tìm nghiệm của đa thức sau
x2 + x
cho biết hai đại lượng x và y tỉ lệ thuận với nhau, và khi x 3,6 thì y -10,8
a/ viết công thức liên hệ giữa x và y
b/ tính giá trị của y khi x -3 ; 24 ; -dfrac{2}{3} ; dfrac{7}{6} ; -dfrac{1}{15}
c/ tính giá trị của x khi y 4 ; 12 ; -26 ; dfrac{4}{3} ; -dfrac{26}{15}
Đọc tiếp
cho biết hai đại lượng x và y tỉ lệ thuận với nhau, và khi x = 3,6 thì y = -10,8
a/ viết công thức liên hệ giữa x và y
b/ tính giá trị của y khi x = -3 ; 24 ; \(-\dfrac{2}{3}\) ; \(\dfrac{7}{6}\) ; \(-\dfrac{1}{15}\)
c/ tính giá trị của x khi y = 4 ; 12 ; -26 ; \(\dfrac{4}{3}\) ; \(-\dfrac{26}{15}\)
Cho đa thức P(x). Giải thích tại sao nếu có đa thức Q(x) sao cho P(x) = (x – 3) . Q(x) (tức là P(x) chia hết cho x – 3) thì x = 3 là một nghiệm của P(x)











