Question

1) C/m đẳng thức

 \(\dfrac{1-2sin\alpha}{sin^2\alpha-cos^2\alpha}=\dfrac{sin\alpha-cos\alpha}{sin\alpha+cos\alpha}\)(α nhọn, α≠45^o)

2) Tính\(\dfrac{sin^210^o+sin^220^o+sin^230^o+sin^240^o+sin^250^o+sin^260^o+sin^270^o+sin^280^o+}{cos^210^o+cos^220^o+cos^230^o+cos^240^o+cos^250^o+cos^260^o+cos^270^o+cos^280^o}\)

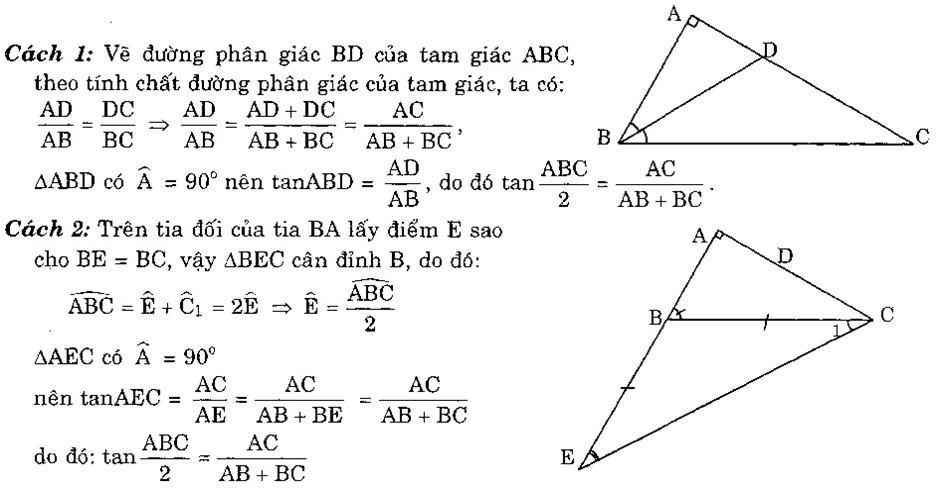
3)Cho tam giác ABC vuông tại A. Chứng minh tan (^ABC)/2= AC/(AB+BC)

 

 

Answer 1

\(1,VT=\dfrac{\left(sina-cosa\right)\left(sina-cosa\right)}{\left(sina+cosa\right)\left(sina-cosa\right)}=\dfrac{\left(sina-cosa\right)^2}{sin^2a+cos^2a}=\dfrac{sin^2a-2sina.cosa+cos^2a}{sin^2a+cos^2a}=\dfrac{1-2sina.cosa}{sin^2a+cos^2}\)

Answer 2

Làm đúng và đủ câu này sẽ đc tick , tặng 2 coin

Answer 3

Tham khảo câu 3 ạ

Answer 4

Ta có : \(\sin\alpha=\cos\beta\); với \(\left(\alpha+\beta=90\right)\)

\(\Rightarrow\sin^2\alpha=\cos^2\beta\)

Khi đó \(P=\dfrac{sin^210+sin^220+...+sin^280}{cos^210+cos^220+...+cos^280}=\dfrac{cos^280+cos^270+...+cos^210}{cos^210+cos^220+...+cos^280}=1\)