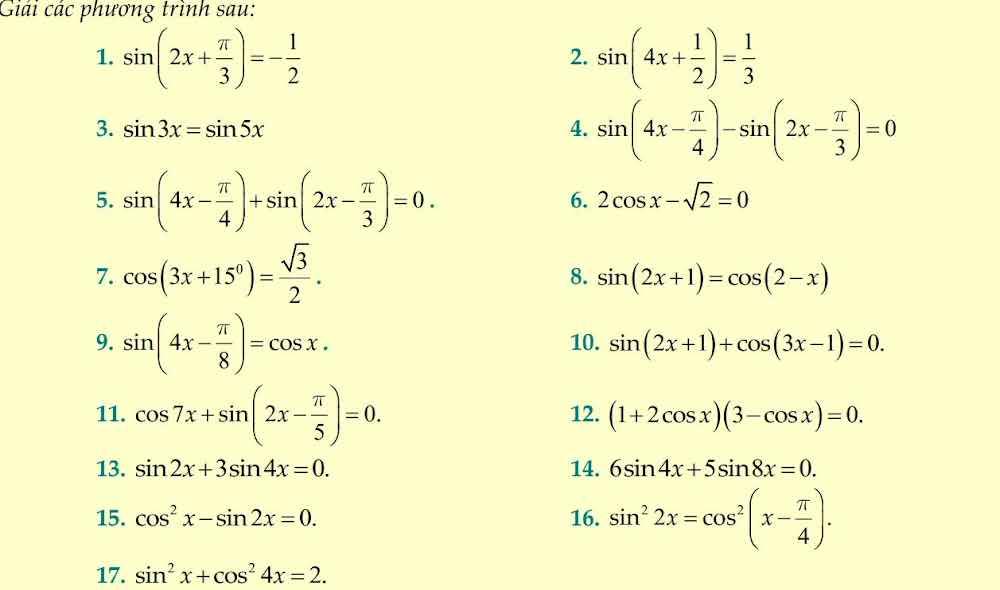1: \(sin\left(2x+\dfrac{\Omega}{3}\right)=-\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{3}=-\dfrac{\Omega}{6}+k2\Omega\\2x+\dfrac{\Omega}{3}=\dfrac{7}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\Omega}{2}+k2\Omega\\2x=\dfrac{5}{6}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{\Omega}{4}+k\Omega\\x=\dfrac{5}{12}\Omega+k\Omega\end{matrix}\right.\)
2: sin(4x+1/2)=1/3
=>\(\left[{}\begin{matrix}4x+\dfrac{1}{2}=arcsin\left(\dfrac{1}{3}\right)+k2\Omega\\4x+\dfrac{1}{2}=\Omega-arcsin\left(\dfrac{1}{3}\right)+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}4x=arcsin\left(\dfrac{1}{3}\right)+k2\Omega-\dfrac{1}{2}\\4x=\Omega-arcsin\left(\dfrac{1}{3}\right)+k2\Omega-\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{4}\cdot arcsin\left(\dfrac{1}{3}\right)+\dfrac{k\Omega}{2}-\dfrac{1}{8}\\x=\dfrac{\Omega}{4}-\dfrac{1}{4}\cdot arcsin\left(\dfrac{1}{3}\right)+\dfrac{k\Omega}{2}-\dfrac{1}{8}\end{matrix}\right.\)
3: sin 5x=sin 3x
=>\(\left[{}\begin{matrix}5x=3x+k2\Omega\\5x=\Omega-3x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=k2\Omega\\8x=\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=k\Omega\\x=\dfrac{\Omega}{8}+\dfrac{k\Omega}{4}\end{matrix}\right.\)
4:
\(sin\left(4x-\dfrac{\Omega}{4}\right)-sin\left(2x-\dfrac{\Omega}{3}\right)=0\)
=>\(sin\left(4x-\dfrac{\Omega}{4}\right)=sin\left(2x-\dfrac{\Omega}{3}\right)\)
=>\(\left[{}\begin{matrix}4x-\dfrac{\Omega}{4}=2x-\dfrac{\Omega}{3}+k2\Omega\\4x-\dfrac{\Omega}{4}=\dfrac{4}{3}\Omega-2x+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=-\dfrac{1}{12}\Omega+k2\Omega\\6x=\dfrac{19}{12}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{24}\Omega+k\Omega\\x=\dfrac{19}{72}\Omega+\dfrac{k\Omega}{3}\end{matrix}\right.\)
mn ơi hướng dẫn các bài tập này với ạ mình đang cần gấp ạ, milk cảm nhiều ạ