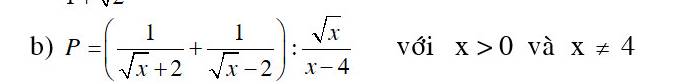\(P=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}:\dfrac{\sqrt{x}}{x-4}\)
\(=\dfrac{2\sqrt{x}}{x-4}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}}=2\)
\(P=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}}{x-4}\) (ĐK: \(x>0;x\ne4\))
\(P=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]:\dfrac{\sqrt{x}}{x-4}\)
\(P=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(P=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}\right)^2-2^2}{\sqrt{x}}\)
\(P=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{x}}\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}}\)
\(P=\dfrac{2}{1}\)
\(P=2\)