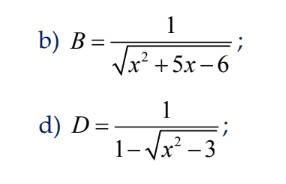\(b,B=\dfrac{1}{\sqrt{x^2+5x-6}}\) xác định \(\Leftrightarrow x^2+5x-6>0\)
\(\Leftrightarrow x^2-x+6x-6>0\\ \Leftrightarrow x\left(x-1\right)+6\left(x-1\right)>0\\ \Leftrightarrow\left(x-1\right)\left(x+6\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1>0\\x+6>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1< 0\\x+6< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>1\\x>-6\end{matrix}\right.\\\left\{{}\begin{matrix}x< 1\\x< -6\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>1\\x< -6\end{matrix}\right.\)
\(d,D=\dfrac{1}{1-\sqrt{x^2-3}}\) xác định \(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{x^2-3}>0\\x^2-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-3}>1\\x^2\ne3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{\left(x^2-3\right)^2}>1\\x\ne\pm\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>2\\x>\sqrt{2}\end{matrix}\right.\\x\ne\pm\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>2\\x\ne\pm\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow x>2\)