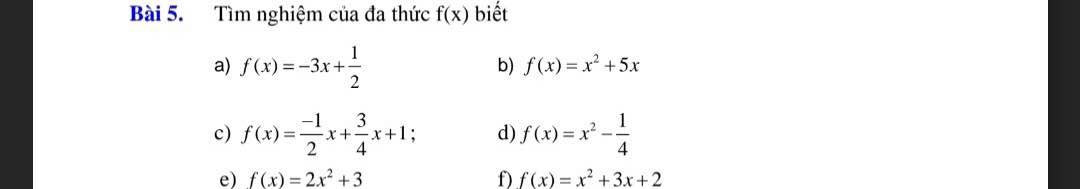`5,`
`a,`
Đặt `A(x)=2x-1=0`
`-> 2x=1`
`-> x=1/2`
Vậy, nghiệm của đa thức là `x=1/2.`
`b,`
Đặt `B(x)=3-6/5x=0`
`-> 6/5x=3-0`
`-> 6/5x=3`
`-> x= 3 \div 6/5`
`-> x=5/2`
Vậy, nghiệm của đa thức là `x=5/2.`
`c,`
Đặt `C(x)=4x^2-25=0`
`-> 4x^2=25`
`-> x^2=25 \div 4`
`-> x^2=25/4`
`-> x^2=(+-5/2)^2`
`-> x=+-5/2`
Vậy, nghiệm của đa thức là `x=5/2 ; x=-5/2.`
`d,`
Đặt `D(x)=(x+1/4)^2-16/9=0`
`-> (x+1/4)^2=16/9`
`-> (x+1/4)^2=(+-4/3)^2`
`->`\(\left[{}\begin{matrix}x+\dfrac{1}{4}=\dfrac{4}{3}\\x+\dfrac{1}{4}=-\dfrac{4}{3}\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=\dfrac{4}{3}-\dfrac{1}{4}\\x=-\dfrac{4}{3}-\dfrac{1}{4}\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=\dfrac{13}{12}\\x=-\dfrac{19}{12}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x=13/12, x=-19/12.`
`e,`
Đặt `E(x)=8x^3+27=0`
`-> 8x^3=-27`
`-> x^3=-27 \div 8`
`->x^3=-27/8`
`-> x^3=(-3/2)^3`
`-> x=-3/2`
Vậy, nghiệm của đa thức là `x=-3/2.`
`f,`
Đặt `F(x)=x^2+3x=0`
`-> x*x+3x=0`
`-> x(x+3)=0`
`->`\(\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\x=0-3\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x=0, x=-3.`