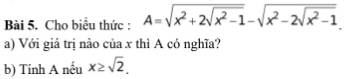ĐKXĐ: \(\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)
Khi \(x\ge\sqrt{2}\Rightarrow\sqrt{x^2-1}\ge1\Rightarrow\sqrt{x^2-1}-1\ge0\)
Do đó:
\(A=\sqrt{x^2-1+2\sqrt{x^2-1}+1}-\sqrt{x^2-1-2\sqrt{x^2-1}+1}\)
\(=\sqrt{\left(\sqrt{x^2-1}+1\right)^2}-\sqrt{\left(\sqrt{x^2-1}-1\right)^2}\)
\(=\left|\sqrt{x^2-1}+1\right|-\left|\sqrt{x^2-1}-1\right|\)
\(=\sqrt{x^2-1}+1-\left(\sqrt{x^2-1}-1\right)\)
\(=2\)
Đúng 1
Bình luận (0)
