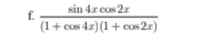6:
b: \(=\dfrac{sina\left(2cosa+1\right)}{1+2cos^2a-1+cosa}\)
\(=\dfrac{sina\left(2cosa+1\right)}{cosa\left(2cosa+1\right)}=\dfrac{sina}{cosa}=tana\)
c: \(=\dfrac{\dfrac{sin2a}{cos2a}\cdot\dfrac{sina}{cosa}}{\dfrac{sin2a}{cos2a}-\dfrac{sina}{cosa}}\)
\(=\dfrac{sin2a\cdot sina}{sin2a\cdot cosa-sina\cdot cos2a}\)
\(=\dfrac{sina^2\cdot2\cdot cosa}{sina\cdot cos^2a\cdot2-sina\cdot\left(2cos^2a-1\right)}\)
\(=\dfrac{sin^2a\cdot2\cdot cosa}{sina\left(2cos^2a-2cos^2a+1\right)}=2\cdot sina\cdot cosa=sin2a\)