\(P=\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2-2\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2\)
\(=2\overrightarrow{MO}\left(\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}\right)=2\overrightarrow{MO}\left(\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{AO}+\overrightarrow{OC}\right)\)
\(=2\overrightarrow{MO}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=4\overrightarrow{MO}.\overrightarrow{AN}\) (trong đó N là trung điểm BC)
\(=4MO.AN.cos\left(\overrightarrow{MO};\overrightarrow{AN}\right)\)
Do tam giác ABC cố định \(\Rightarrow MO=R\) cố định và \(AN\) cố định
\(\Rightarrow P_{min}\) khi \(cos\left(\overrightarrow{MO};\overrightarrow{AN}\right)\) đạt min \(\Rightarrow cos\left(\overrightarrow{MO};\overrightarrow{AN}\right)=-1\)
\(\Rightarrow\overrightarrow{MO};\overrightarrow{AN}\) là 2 vecto cùng phương ngược chiều
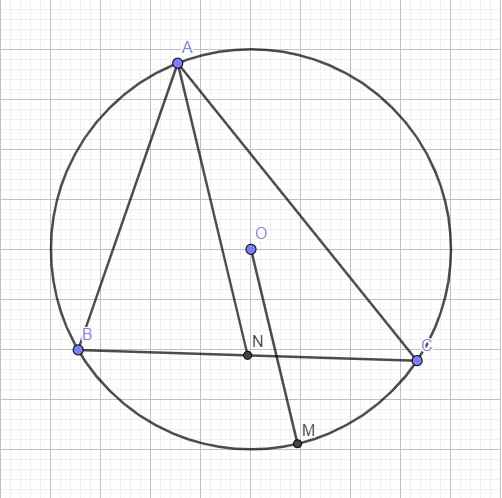
\(\Rightarrow\) M là giao điểm của đường thẳng qua O và song song AN sao cho M và A nằm trên 2 nửa mp khác nhau bờ BC