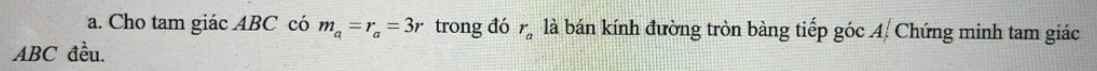Ta có: \(\left\{{}\begin{matrix}r_a=p.tan\dfrac{A}{2}\\r=\left(p-a\right)tan\dfrac{A}{2}\end{matrix}\right.\) \(\Rightarrow p=3\left(p-a\right)\)
\(\Rightarrow3a=2p=a+b+c\)
\(\Rightarrow b+c=2a\)
Lại có: \(m_a=3r\Rightarrow m_a^2=9r^2=\dfrac{9S^2}{p^2}\)
\(\Rightarrow\dfrac{2b^2+2c^2-a^2}{4}=\dfrac{9p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p^2}\)
\(\Rightarrow2b^2+2c^2-a^2=\dfrac{9\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}{a+b+c}\) (1)
Do \(b+c=2a\Rightarrow\dfrac{b+c-a}{a+b+c}=\dfrac{2a-a}{a+2a}=\dfrac{1}{3}\)
Đồng thời: \(\left(a+b-c\right)\left(c+a-b\right)=\dfrac{\left(3b-c\right)\left(3c-b\right)}{4}\)
Thay vào (1):
\(8b^2+8c^2-\left(b+c\right)^2=3\left(3b-c\right)\left(3c-b\right)\)
\(\Leftrightarrow16\left(b-c\right)^2=0\)
\(\Leftrightarrow b=c\)
Thay vào \(2a=b+c\Rightarrow a=b=c\)
Vậy tam giác ABC đều