Bài này kết quả phụ thuộc rất nhiều vào... mắt người nhìn
Từ đồ thị \(f'\left(x\right)\) kia, theo em thì phần diện tích giới hạn màu đỏ lớn hay màu xanh lớn? Nó sẽ quyết định đáp án

Nếu phần diện tích màu đỏ lớn hơn màu xanh:
\(\Rightarrow\int\limits^1_0\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\)
\(\Rightarrow\int\limits^1_0f'\left(x\right)dx>-\int\limits^2_1f'\left(x\right)dx\) (do trên \(\left(1;2\right)\) f'(x) mang dấu âm)
\(\Rightarrow f\left(1\right)-f\left(0\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(0\right)< f\left(2\right)\)
Từ đó và bảng xét dấu của \(f'\left(x\right)\), ta có BBT của \(f\left(x\right)\) như sau:
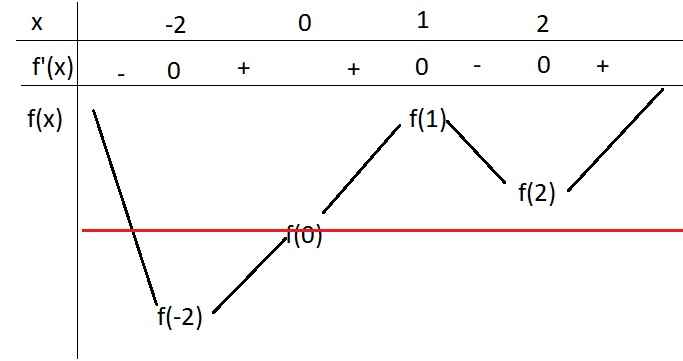
Do \(f\left(0\right)< f\left(2\right)\) nên \(f\left(0\right)\) nằm thấp hơn \(f\left(2\right)\), do đó đường thẳng \(y=f\left(0\right)\) cắt \(y=f\left(x\right)\) có dạng như hình trên.
Ta thấy ngay pt \(f\left(x\right)=f\left(0\right)\) chỉ có 2 nghiệm
Ngược lại, nếu em nhìn thấy phần màu xanh có diện tích lớn hơn màu đỏ
\(\Rightarrow\int\limits^1_0\left|f'\left(x\right)\right|dx< \int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow f\left(1\right)-f\left(0\right)< f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(0\right)>f\left(2\right)\)
Khi đó thì tương giao nó lại dạng thế này:
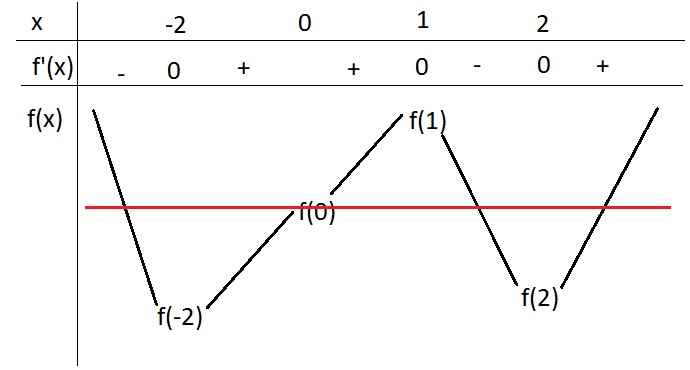
Ta thấy ngay \(f\left(x\right)=f\left(0\right)\) có 4 nghiệm
Kiểu bài dựa trên diện tích lớn - nhỏ của các phần đồ thị này xuất hiện khá nhiều. Thường người ta sẽ cho các phần đồ thị lớn nhỏ rõ ràng trực quan nhìn là thấy cái nào lớn hơn ngay.















