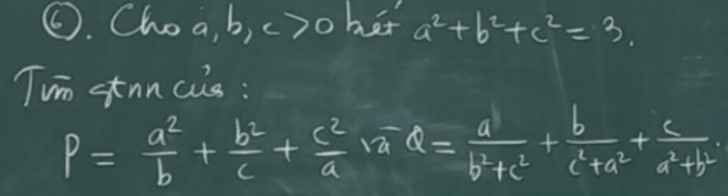1. Tìm min P:
Cách 1: nhanh nhất là chúng ta sử dụng BĐT Holder:
\(\left(\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\right)\left(\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\right)\left(a^2b^2+b^2c^2+c^2a^2\right)\ge\left(a^2+b^2+c^2\right)^3\)
\(=\left(a^2+b^2+c^2\right)\left(a^2+b^2+c^2\right)^2\ge\left(a^2+b^2+c^2\right).3\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(\Rightarrow P^2\ge3\left(a^2+b^2+c^2\right)=9\)
\(\Rightarrow P\ge3\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Nếu không sử dụng Holder, ta làm như sau:
\(P^2=\left(\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\right)^2=\dfrac{a^4}{b^2}+\dfrac{b^4}{c^2}+\dfrac{c^4}{a^2}+\dfrac{2a^2b}{c}+\dfrac{2b^2c}{a}+\dfrac{2c^2a}{b}\)
\(P^2=\left(\dfrac{a^4}{b^2}+\dfrac{a^2b}{c}+\dfrac{a^2b}{c}+c^2\right)+\left(\dfrac{b^4}{c^2}+\dfrac{b^2c}{a}+\dfrac{b^2c}{a}+a^2\right)+\left(\dfrac{c^4}{a^2}+\dfrac{c^2a}{b}+\dfrac{c^2a}{b}+b^2\right)-3\)
\(P^2\ge4\sqrt[4]{\dfrac{a^8b^2c^2}{b^2c^2}}+4\sqrt[4]{\dfrac{b^8a^2c^2}{a^2c^2}}+4\sqrt[4]{\dfrac{c^8a^2b^2}{a^2b^2}}-3\)
\(P^2\ge4\left(a^2+b^2+c^2\right)-3=9\)
\(\Rightarrow P\ge3\)
Dấu "=" xảy ra khi \(a=b=c=1\)
\(Q=\dfrac{a}{b^2+c^2}+\dfrac{b}{c^2+a^2}+\dfrac{c}{a^2+b^2}=\dfrac{a}{3-a^2}+\dfrac{b}{3-b^2}+\dfrac{c}{3-c^2}\)
Ta có:
\(a^3+1+1\ge3a\Leftrightarrow2\ge a\left(3-a^2\right)\)
\(\Rightarrow\dfrac{1}{3-a^2}\ge\dfrac{a}{2}\Rightarrow\dfrac{a}{3-a^2}\ge\dfrac{a^2}{2}\)
Tương tự:
\(\dfrac{b}{3-b^2}\ge\dfrac{b^2}{2}\) ; \(\dfrac{c}{3-c^2}\ge\dfrac{c^2}{2}\)
Cộng vế:
\(Q\ge\dfrac{a^2+b^2+c^2}{2}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)