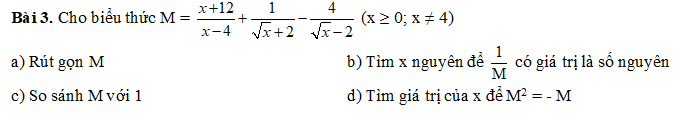\(a,M=\dfrac{x+12+\sqrt{x}-2-4\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\\ b,\dfrac{1}{M}=\dfrac{\sqrt{x}-1+3}{\sqrt{x}-1}=1+\dfrac{3}{\sqrt{x}-1}\in Z\\ \Leftrightarrow\sqrt{x}-1\inƯ\left(3\right)=\left\{-1;1;3\right\}\left(\sqrt{x}-1\ge-1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(x\ne4\right)\\ c,M=\dfrac{\sqrt{x}+2-3}{\sqrt{x}+2}=1-\dfrac{3}{\sqrt{x}+2}< 1\left(\dfrac{3}{\sqrt{x}+2}>0\right)\\ d,M^2=-M\Leftrightarrow M^2+M=0\Leftrightarrow M\left(M+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}M=0\\M=-1\end{matrix}\right.\)
Với \(M=0\Leftrightarrow\sqrt{x}-1=0\Leftrightarrow x=1\left(tm\right)\)
Với \(M=-1\Leftrightarrow\sqrt{x}-1=-\sqrt{x}-2\Leftrightarrow2\sqrt{x}=-1\Leftrightarrow x\in\varnothing\)