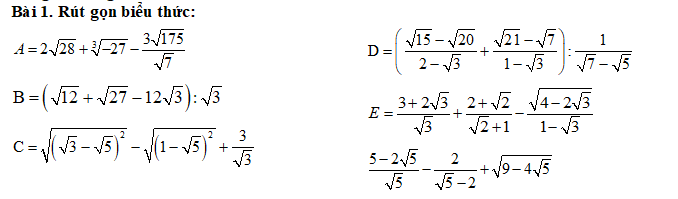\(A=4\sqrt{7}-3-15=4\sqrt{7}-18\\ B=\left(2\sqrt{3}+3\sqrt{3}-12\sqrt{3}\right):\sqrt{3}=-7\sqrt{3}:\sqrt{3}=-7\\ C=\sqrt{5}-\sqrt{3}-\sqrt{5}+1+\sqrt{3}=1\\ D=\left[\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{2-\sqrt{3}}+\dfrac{\sqrt{7}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]\left(\sqrt{7}-\sqrt{5}\right)=\left(-\sqrt{7}-\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=-\left(7-5\right)=-2\\ E=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\dfrac{\sqrt{3}-1}{1-\sqrt{3}}=\sqrt{3}+\sqrt{2}+1\\ F=\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{\sqrt{5}}-\dfrac{2\left(\sqrt{5}+2\right)}{1}+\sqrt{\left(2-\sqrt{5}\right)^2}=\sqrt{5}-2-2\sqrt{5}-4+2-\sqrt{5}=-4-2\sqrt{5}\)
Bài 2: Hệ hai phương trình bậc nhất hai ẩn. Luyện tập
Đúng 3
Bình luận (0)
Các câu hỏi tương tự
giải hệ phương trình
x(x+y)=6
và x^3+y^3+18y=27
giải HPT
\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{3}{y}=-1\\\dfrac{3}{x}-\dfrac{2}{y}=5\end{matrix}\right.\)
Cuối học kỳ, một học sinh có 11 bài kiểm tra đạt các điểm 8, 9, 10. Biết tổng điểm các bài kiểm tra là 100. Hỏi học sinh đó có bao nhiêu bài kiểm tra đạt điểm 8, điểm 9, điểm 10
ai giúp vs ạ,tí nộp r
\(\left\{{}\begin{matrix}2\text{x}+y=5m-1\\x-2y=2\end{matrix}\right.\)(m là tham số)
tìm m để pt có 2 nghiệm thỏa mãn \(x^2-2y^2=-2\)
Giải hê phương trình
x+y+z =11
2x-y+z=5
3x+2y+z=14
2 tổ sản xuất cùng may 1 loại áo. Tổ 1 may trong 3 ngày. Tổ 2 may trong 5 ngày được 1310 chiếc áo. Mỗi ngày tổ 1 may nhiều hơn tổ 2 10 áo. Hỏi trong 1 ngày mỗi tổ may bao nhiêu?
Giải hệ phương trình \(\left\{{}\begin{matrix}x+3y+5=xy\\\frac{1}{x-1}+\frac{1}{y-2}=2\end{matrix}\right.\)
Cho x,y tm \(4(x\sqrt{y-16} + y\sqrt{x-16}) = xy\)Tính giá trị của biểu thức
A= (x-33)^2019 + (y-31)^2020