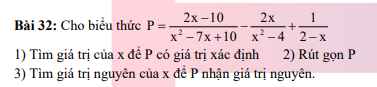\(1,ĐK:x\ne\pm2;x\ne5\\ 2,P=\dfrac{2}{x-2}-\dfrac{2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\\ P=\dfrac{1}{x-2}-\dfrac{2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2-2x}{\left(x-2\right)\left(x+2\right)}\\ P=\dfrac{2-x}{\left(x-2\right)\left(x+2\right)}=\dfrac{-1}{x+2}\\ 3,P\in Z\Leftrightarrow x+2\inƯ\left(-1\right)=\left\{-1;1\right\}\\ \Leftrightarrow x\in\left\{-3;-1\right\}\left(tm\right)\)
1) \(ĐKXĐ:x\ne2;x\ne-2;x\ne5.\)
2) \(P=\dfrac{2x-10}{x^2-7x+10}-\dfrac{2x}{x^2-4}+\dfrac{1}{2-x}\left(ĐKXĐ:x\ne2;x\ne-2;x\ne5\right).\)
\(P=\dfrac{2\left(x-5\right)}{\left(x-5\right)\left(x-2\right)}-\dfrac{2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}.\)
\(P=\dfrac{2}{x-2}-\dfrac{2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}.\)
\(P=\dfrac{2\left(x+2\right)-2x-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}.\)
\(P=\dfrac{2x+4-2x-x-2}{\left(x-2\right)\left(x+2\right)}.\)
\(P=\dfrac{-x+2}{\left(x-2\right)\left(x+2\right)}.\)
\(P=\dfrac{-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}.\)
\(P=\dfrac{-1}{x+2}.\)
3) Để \(P\in Z\) <=> \(\dfrac{-1}{x+2}\in Z\) => \(x+2\inƯ\left(-1\right)\) <=>\(x+2\in\left\{-1;1\right\}\).
TH1: x + 2 = -1 <=> x = -3 (TM).
Th2: x + 2 = 1 <=> x = -1 (TM).
Vậy \(x\in\left\{-3;-1\right\}\).