2.
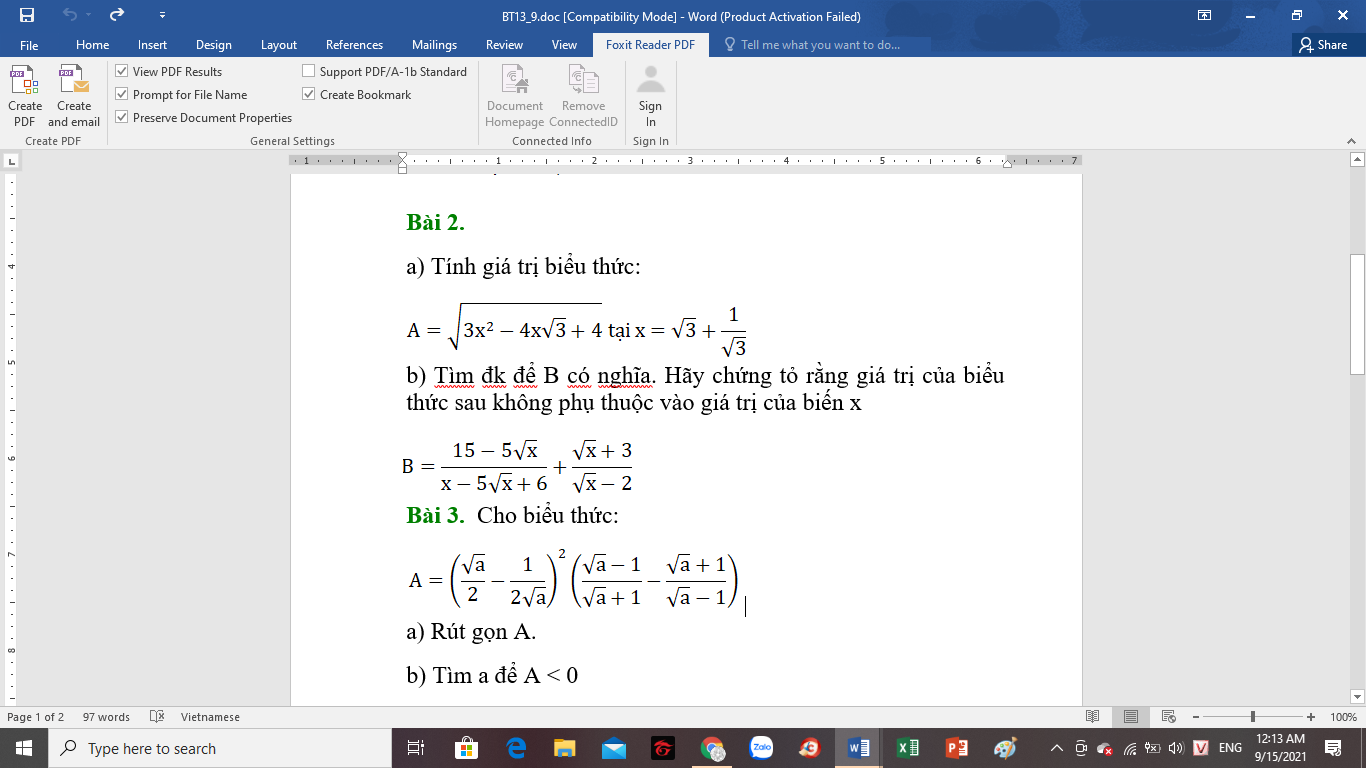
a, \(x=\sqrt{3}+\dfrac{1}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}\)
\(\Rightarrow A=\sqrt{3x^2-4x\sqrt{3}+4}\)
\(=\sqrt{16-16+4}\)
\(=2\)
b, ĐK: \(\left\{{}\begin{matrix}x\ge0\\x-5\sqrt{x}+6\ne0\\\sqrt{x}-2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne4\\x\ne9\end{matrix}\right.\Rightarrow x\ge0;x\ne4;x\ne9\)
\(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{5\left(3-\sqrt{x}\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=-\dfrac{5}{\sqrt{x}-2}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}+3-5}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)
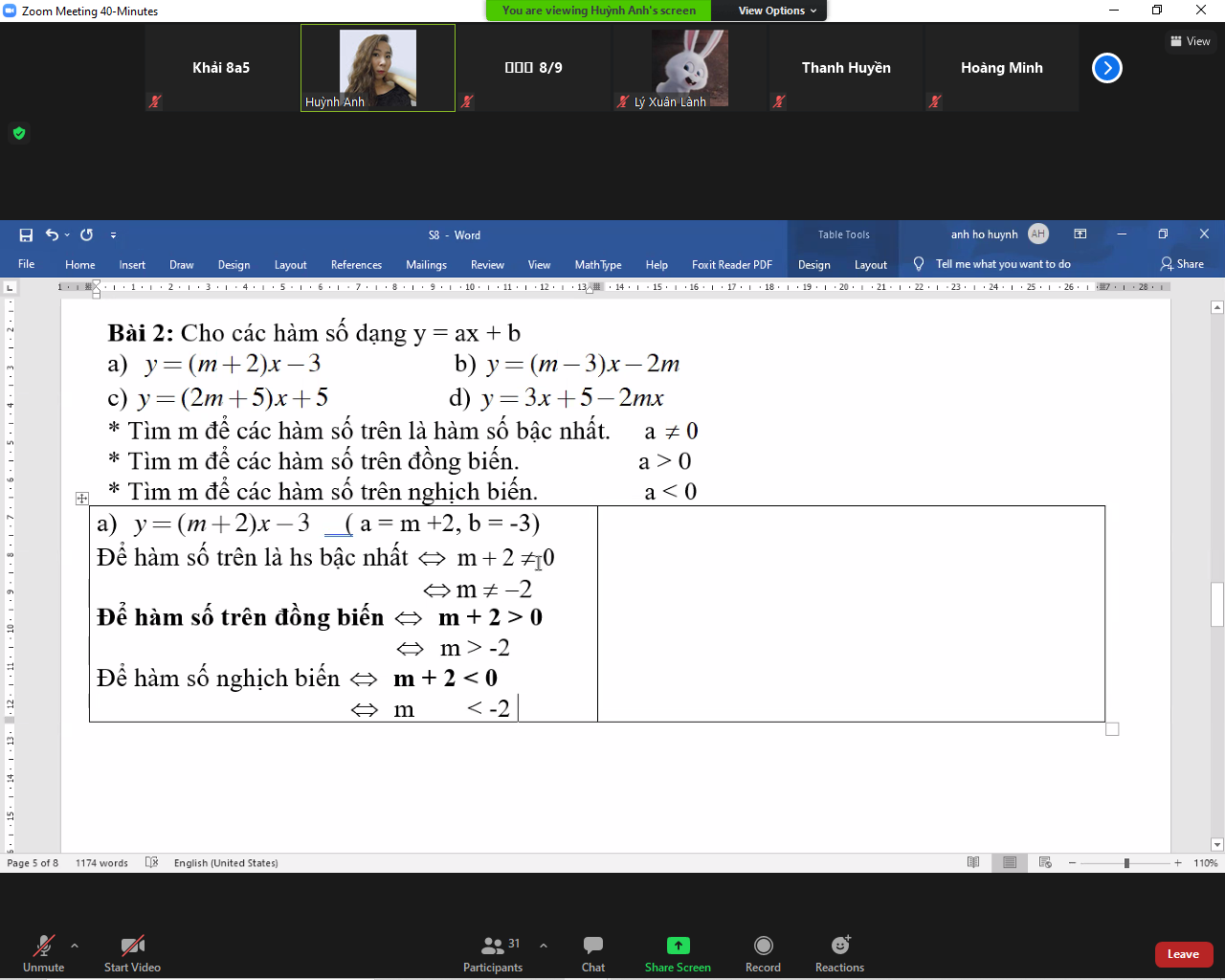
Bài 3:
a. ĐKXĐ: $a>0; a\neq 1$
\(A=\left(\frac{a-1}{2\sqrt{a}}\right)^2.\frac{(\sqrt{a}-1)^2-(\sqrt{a}+1)^2}{(\sqrt{a}-1)(\sqrt{a}+1)}=\frac{(a-1)^2}{4a}.\frac{-4\sqrt{a}}{a-1}=\frac{1-a}{\sqrt{a}}\)
b. $A< 0\Leftrightarrow \frac{1-a}{\sqrt{a}}< 0$
$\Leftrightarrow 1-a< 0$ (do $\sqrt{a}>0$ với mọi $a\in$ ĐKXĐ)
$\Leftrightarrow a>1$
Kết hợp đkxđ suy ra $a>1$ thì $A< 0$