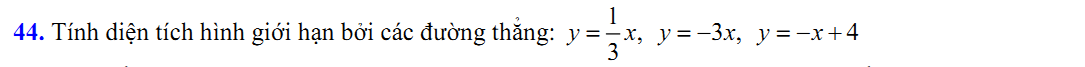Bài 28:
b: Thay x=0 vào \(\left(d1\right)\), ta được:
\(y=2\cdot0+2=2\)
Thay x=0 vào \(\left(d2\right)\), ta được:
\(y=-\dfrac{1}{2}\cdot0-2=-2\)
Phương trình hoành độ giao điểm là:
\(2x+2=-\dfrac{1}{2}x-2\)
\(\Leftrightarrow x\cdot\dfrac{5}{2}=-4\)
hay \(x=-\dfrac{8}{5}\)
Thay \(x=-\dfrac{8}{5}\) vào \(y=2x+2\), ta được:
\(y=2\cdot\dfrac{-8}{5}+2=-\dfrac{6}{5}\)
Vậy: \(A\left(0;2\right)\); \(B\left(0;-2\right)\); \(C\left(-\dfrac{8}{5};-\dfrac{6}{5}\right)\)
\(AB=\sqrt{\left(0-0\right)^2+\left(2+2\right)^2}=4\)
\(AC=\sqrt{\left(0+\dfrac{8}{5}\right)^2+\left(2+\dfrac{6}{5}\right)^2}=\dfrac{8\sqrt{5}}{5}\)
\(BC=\sqrt{\left(0+\dfrac{8}{5}\right)^2+\left(-2+\dfrac{6}{5}\right)^2}=\dfrac{4\sqrt{5}}{5}\)
Vì \(AC^2+BC^2=AB^2\) nên ΔABC vuông tại C
c: Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AC\cdot BC}{2}=\dfrac{\dfrac{8\sqrt{5}}{5}\cdot\dfrac{4\sqrt{5}}{5}}{2}=3.2\left(đvdt\right)\)