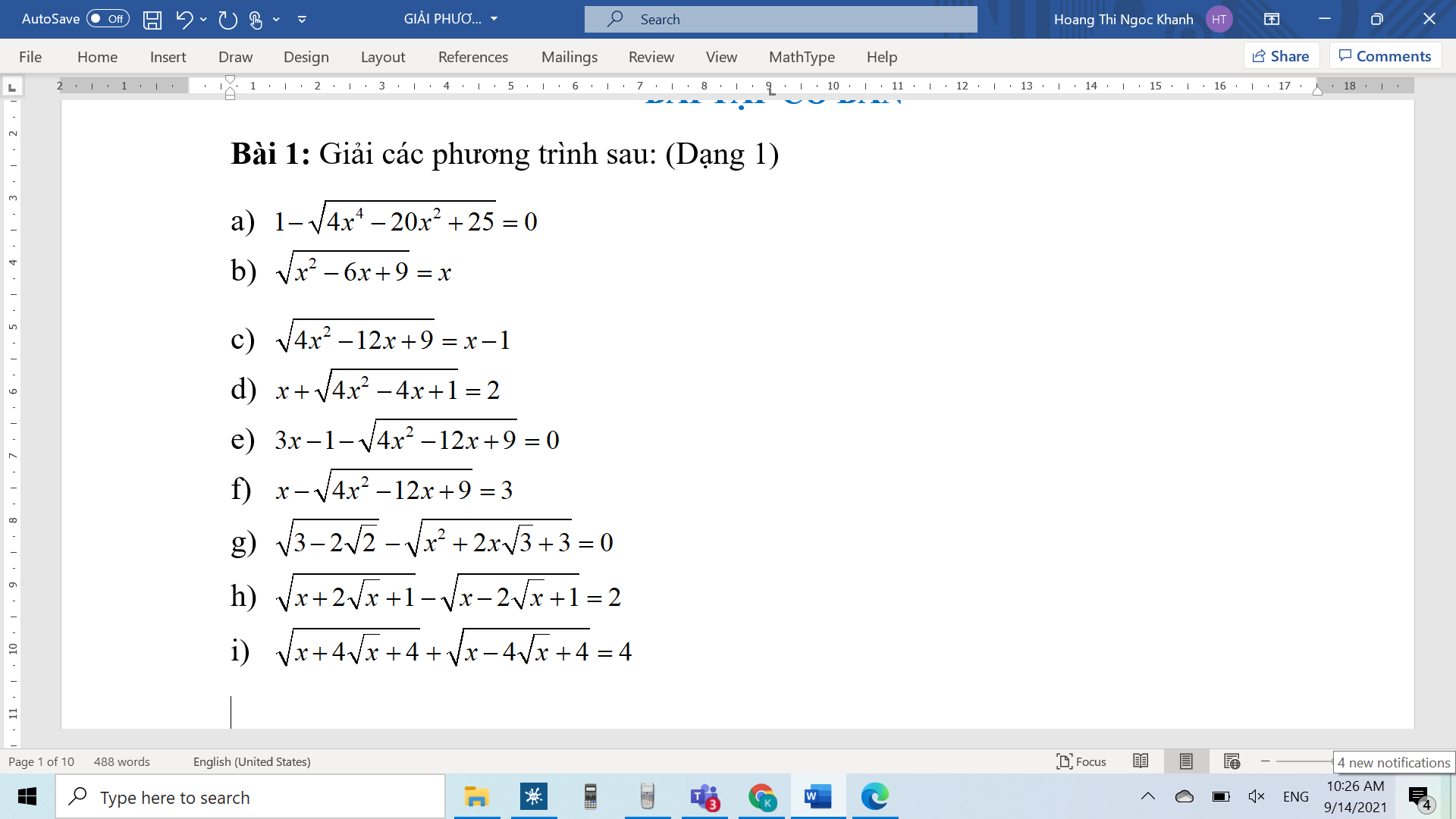
a) \(1-\sqrt{4x^4-20x^2+25}=0\)
\(\Leftrightarrow1-\sqrt{\left(2x^2-5\right)^2}=0\)
\(\Leftrightarrow\left|2x^2-5\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}2x^2-5=1\left(-\sqrt{\dfrac{5}{2}}\ge x\ge\sqrt{\dfrac{5}{2}}\right)\\2x^2-5=-1\left(-\sqrt{\dfrac{5}{2}}< x< \sqrt{\dfrac{5}{2}}\right)\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\sqrt{3}\left(tm\right)\\x=\pm\sqrt{2}\left(tm\right)\end{matrix}\right.\)
b) \(\sqrt{x^2-6x+9}=x\left(đk:x\ge0\right)\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=x\)
\(\Leftrightarrow\left|x-3\right|=x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=x\\x-3=-x\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}0=3\left(vl\right)\\x=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
c) \(\sqrt{4x^2-12x+9}=x-1\left(đk:x\ge1\right)\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=x-1\)
\(\Leftrightarrow\left|2x-3\right|=x-1\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-1\left(x\ge\dfrac{3}{2}\right)\\2x-3=1-x\left(1\le x< \dfrac{3}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\)
d) \(x+\sqrt{4x^2-4x+1}=2\left(đk:x\le2\right)\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=2-x\)
\(\Leftrightarrow\left|2x-1\right|=2-x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=2-x\left(2\ge x\ge\dfrac{1}{2}\right)\\2x-1=x-2\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
e) \(3x-1-\sqrt{4x^2-12x+9}=0\left(đk:x\le\dfrac{1}{3}\right)\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=1-3x\)
\(\Leftrightarrow\left|2x-3\right|=1-3x\)
\(\Leftrightarrow2x-3=3x-1\)( do \(x\le\dfrac{1}{3}\))
\(\Leftrightarrow x=-2\left(tm\right)\)
f) \(x-\sqrt{4x^2-12x+9}=0\left(đk:x\ge0\right)\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=x\)
\(\Leftrightarrow\left|2x-3\right|=x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x\left(x\ge\dfrac{3}{2}\right)\\2x-3=-x\left(0\le x< \dfrac{3}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
g) \(\sqrt{3-2\sqrt{2}}-\sqrt{x^2+2x\sqrt{3}+3}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2}-1\right)^2}-\sqrt{\left(x+\sqrt{3}\right)^2}=0\)
\(\Leftrightarrow\left|x+\sqrt{3}\right|=\sqrt{2}-1\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\sqrt{3}=\sqrt{2}-1\left(x\ge-\sqrt{3}\right)\\x+\sqrt{3}=1-\sqrt{2}\left(x< -\sqrt{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}-1-\sqrt{3}\left(tm\right)\\x=1-\sqrt{2}-\sqrt{3}\left(tm\right)\end{matrix}\right.\)
P/s: Lần sau bạn đăng một lần ít câu thôi nhé! Nhiều như vậy làm đuối lắm