Lời giải:
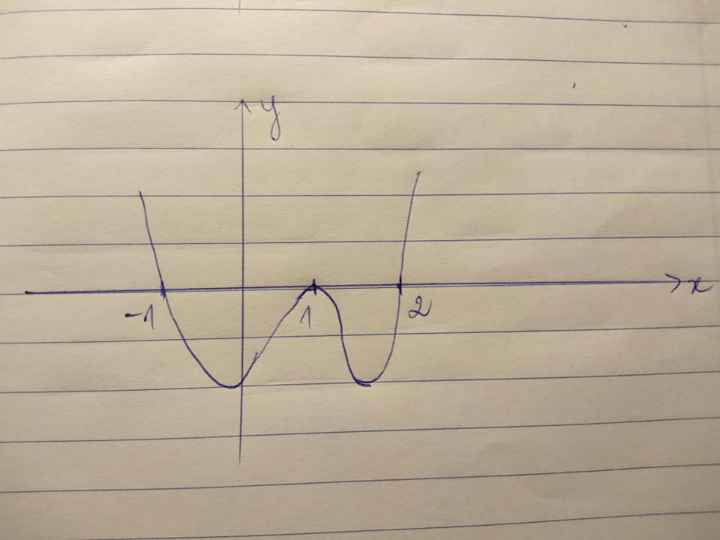
a. Ta thấy hàm số có điểm dừng tại $x=-1; x=0; x=2; x=3$
$f(-1)=1$
$f(0)=2$
$f(2)=-2$
$f(3)=3$
Vậy $f_{\min}=f(2)=-2; f_{\max}=f(3)=3$
b.
Đặt $x^2=t$ thì cần tìm min, max $f(t)$ với $t\in [0;2]$
Theo hình vẽ:
$f(t)_{\min}=f(2)=-2$
$f(t)_{\max}=f(0)=2$
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
Tìm GTLN, GTNN của hàm số :
\(y=sin^3x-cos2x+sinx-1\)
Có bao nhiêu giá trị của m để giá trị lớn nhất của HS y =| -x^4 +8x^2 +m| trên đoạn [-1;3] bằng 2018?
Tìm GTLN cua hàm số y=\(\dfrac{x+\sqrt{1+9x^2}}{8x^2+1}\), x>0
Tìm GTNN của P=\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}-\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)+\dfrac{x}{y}+\dfrac{y}{x}\). Với x, y ≠ 0
Giá trị nhỏ nhất của HS y= 3x +✓10-x^2 bằng? Bài này nếu bấm máy thì bấm như nào ạ?
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
23. Cho hs y= f(x) có đạo hàm f'(x) =-x^2-1 . Với các số thực dương a,b thoả mãn a
