TXĐ: D=R
\(y'=x^2+2x-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}y=+\infty\) ; \(\lim\limits_{x\rightarrow-\infty}y=-\infty\)
BBT:
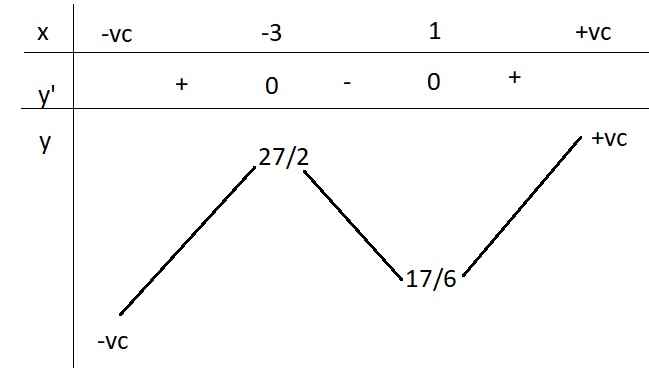
Hàm đồng biến trên các khoảng \(\left(-\infty;-3\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-3;1\right)\)
Hàm đạt cực đại tại \(x=-3;y_{cđ}=\dfrac{27}{2}\)
Hàm đạt cực tiểu tại \(x=1;y_{ct}=\dfrac{17}{6}\)
Đồ thị:
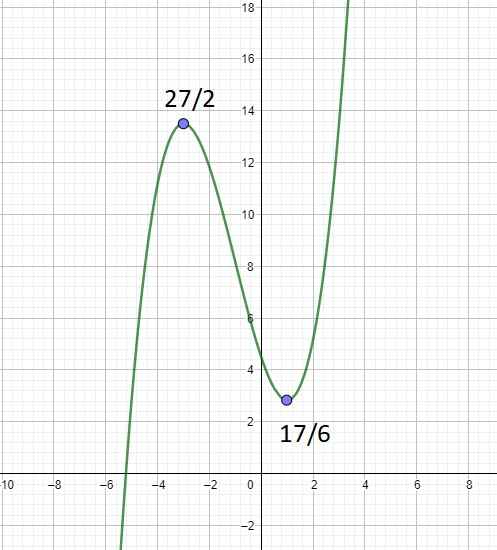
b.
\(2x^3+6x^2-18x-k=0\)
\(\Leftrightarrow\dfrac{1}{3}x^3+x^2-3x=\dfrac{k}{6}\)
\(\Leftrightarrow\dfrac{1}{3}x^3+x^2-3x+\dfrac{9}{2}=\dfrac{k}{6}+\dfrac{9}{2}\)
Từ đồ thị ta thấy đường thẳng \(y=\dfrac{k}{6}+\dfrac{9}{2}\) cắt \(y=\dfrac{1}{3}x^3+x^2-3x+\dfrac{9}{2}\) tại 3 điểm phân biệt khi và chỉ khi:
\(\dfrac{17}{6}< \dfrac{k}{6}+\dfrac{9}{2}< \dfrac{27}{2}\)
\(\Leftrightarrow-10< k< 54\)
c.
Do tiếp tuyến vuông góc \(y=-\dfrac{1}{5}x+2\Rightarrow\) tiếp tuyến có hsg k thỏa mãn:
\(k\left(-\dfrac{1}{5}\right)=-1\Rightarrow k=5\)
Gọi hoành độ tiếp điểm là \(x_0\Rightarrow y'\left(x_0\right)=5\)
\(\Rightarrow x_0^2+2x_0-3=5\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{31}{6}\\x_0=-4\Rightarrow y_0=\dfrac{67}{6}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=5\left(x-2\right)+\dfrac{31}{6}\\y=5\left(x+4\right)+\dfrac{67}{6}\end{matrix}\right.\)