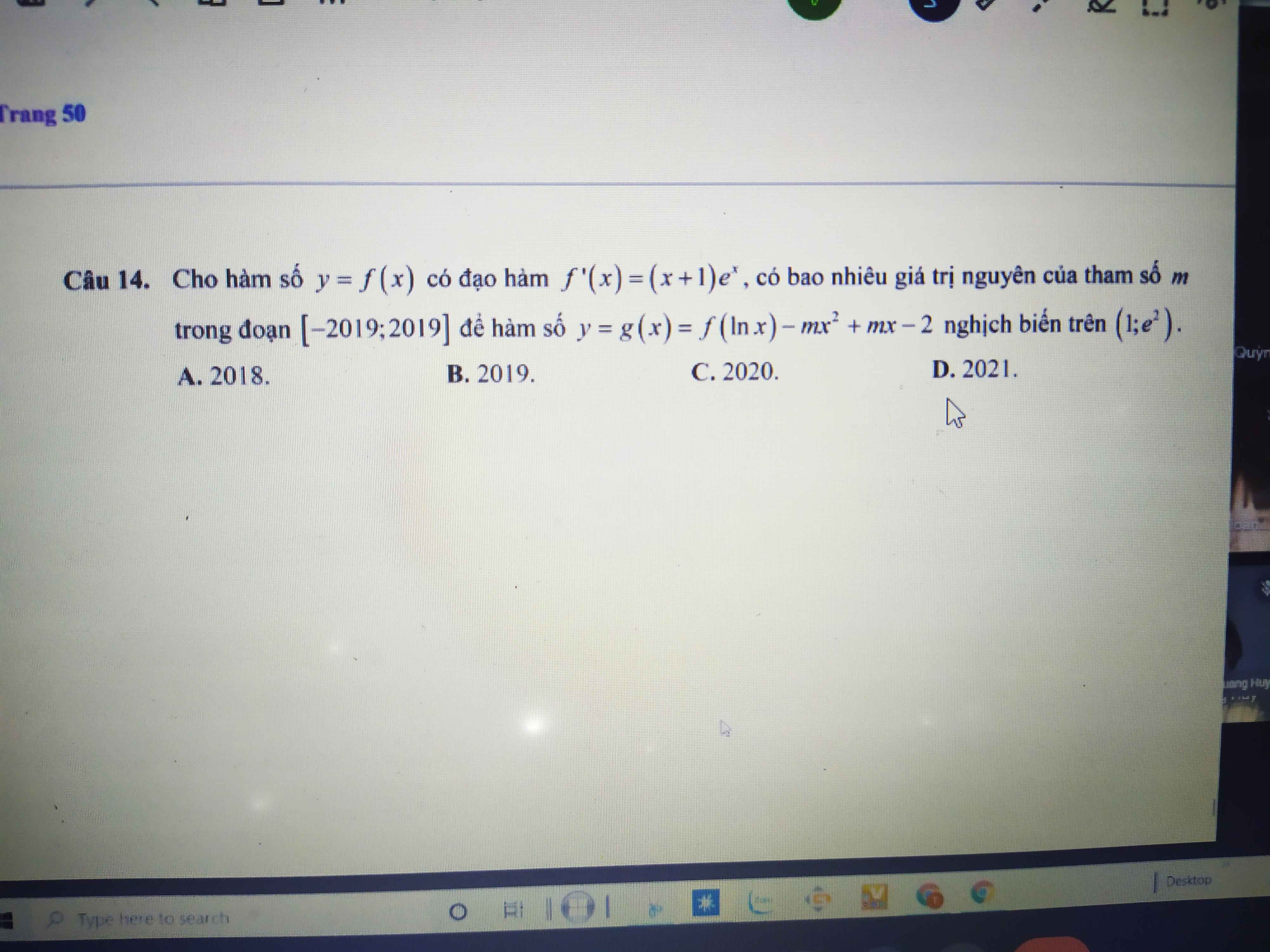
\(g'\left(x\right)=\dfrac{1}{x}f'\left(lnx\right)-2mx+m=\dfrac{1}{x}\left[f'\left(lnx\right)-m\left(2x^2-x\right)\right]\)
Trên \(\left(1;e^2\right)\Rightarrow2x^2-x\) đồng biến \(\Rightarrow2x^2-x>f\left(1\right)=1>0\)
Do đó: \(f'\left(lnx\right)-m\left(2x^2-x\right)\le0\Leftrightarrow f'\left(lnx\right)\le m\left(2x^2-x\right)\)
\(\Leftrightarrow m\ge\dfrac{f'\left(lnx\right)}{2x^2-x}=\dfrac{\left(lnx+1\right)e^{lnx}}{2x^2-x}=\dfrac{\left(lnx+1\right).x}{2x^2-x}=\dfrac{lnx+1}{2x-1}\)
Xét hàm \(h\left(x\right)=\dfrac{lnx+1}{2x-1}\) trên \(\left(1;e^2\right)\)
\(h'\left(x\right)=-\dfrac{2x.lnx+1}{x\left(2x-1\right)^2}< 0\Rightarrow h\left(x\right)\) nghịch biến
\(\Rightarrow h\left(x\right)< h\left(1\right)=1\)
\(\Rightarrow m\ge1\)