Question

Answer 1

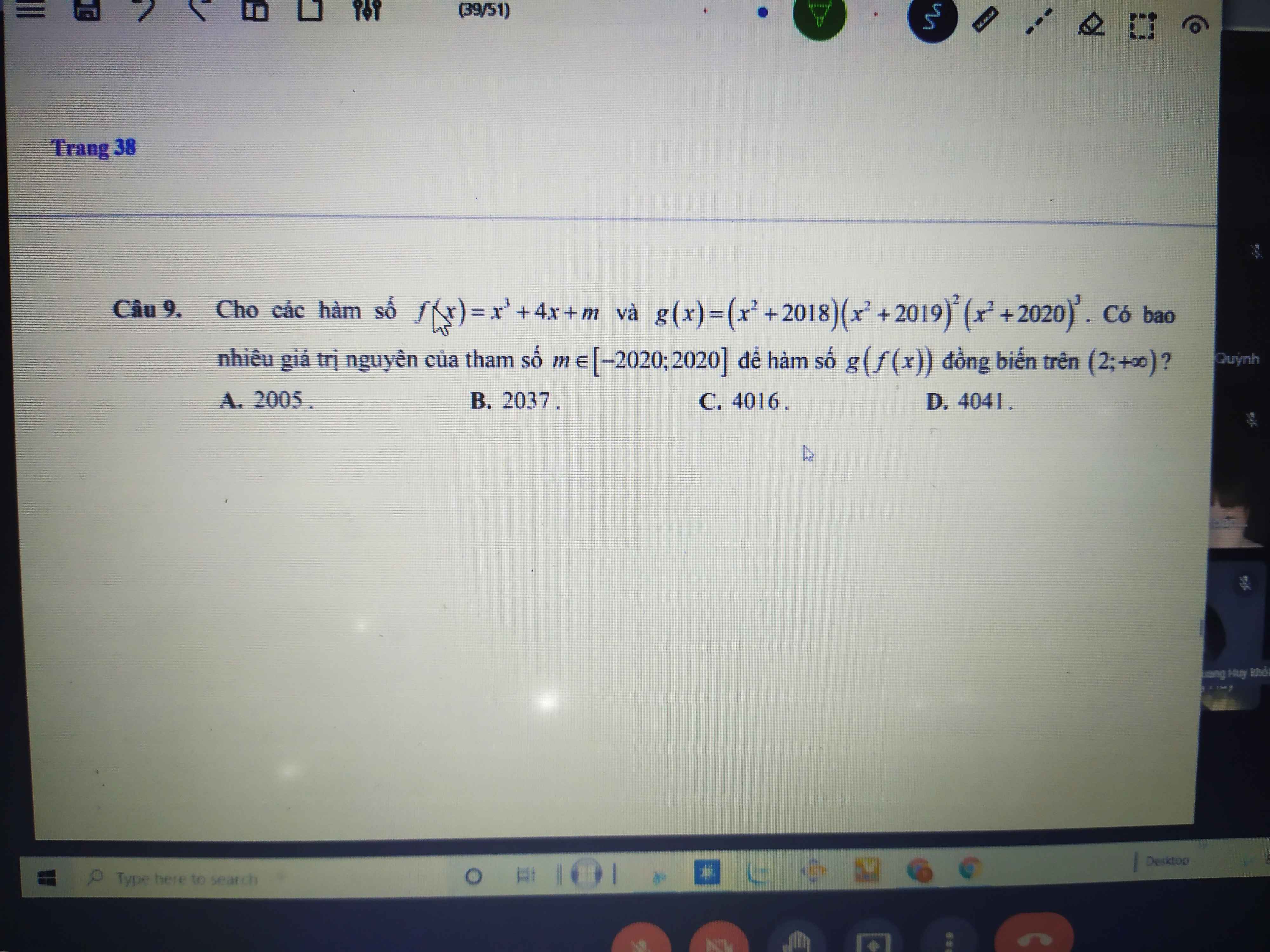
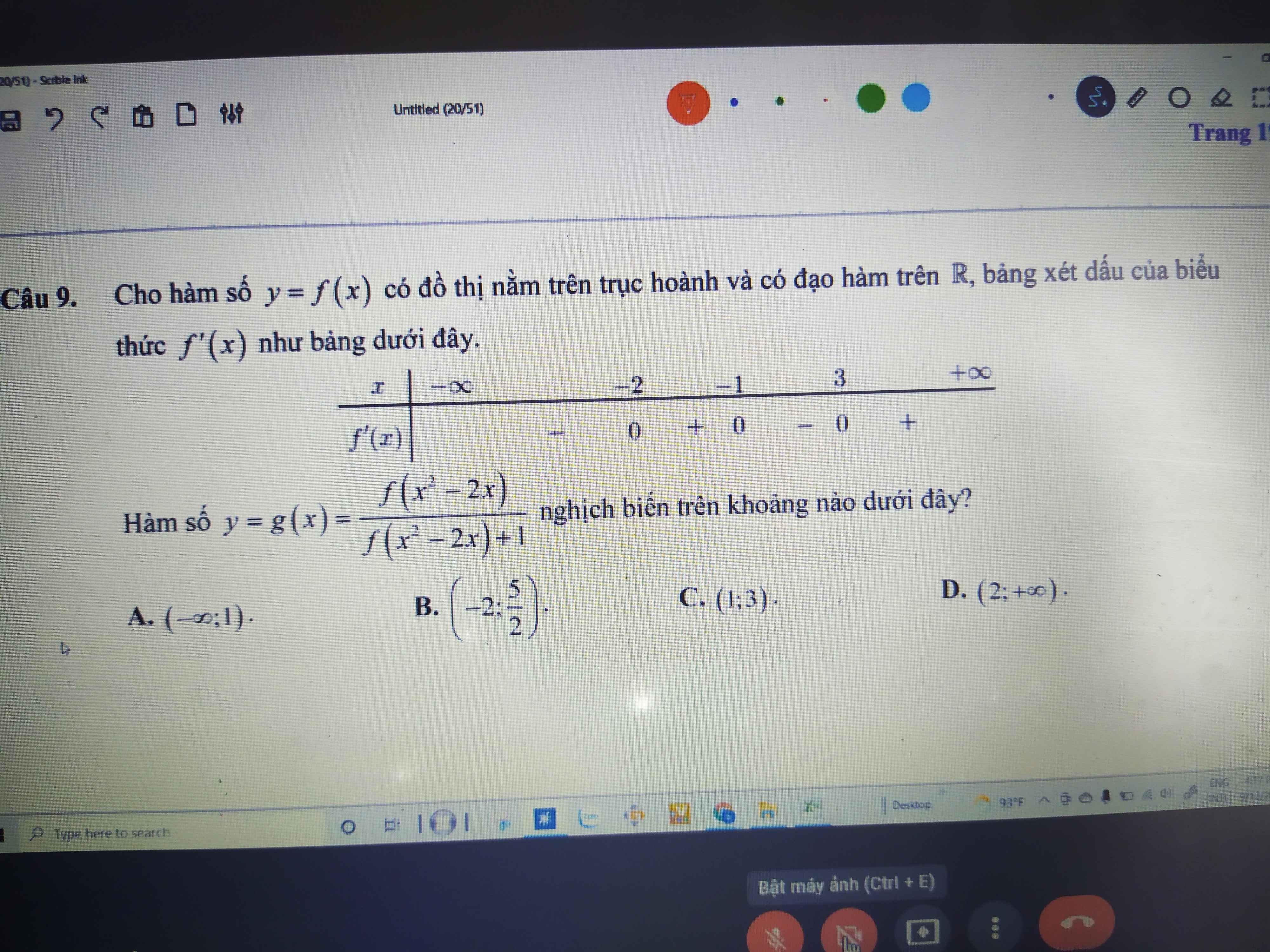
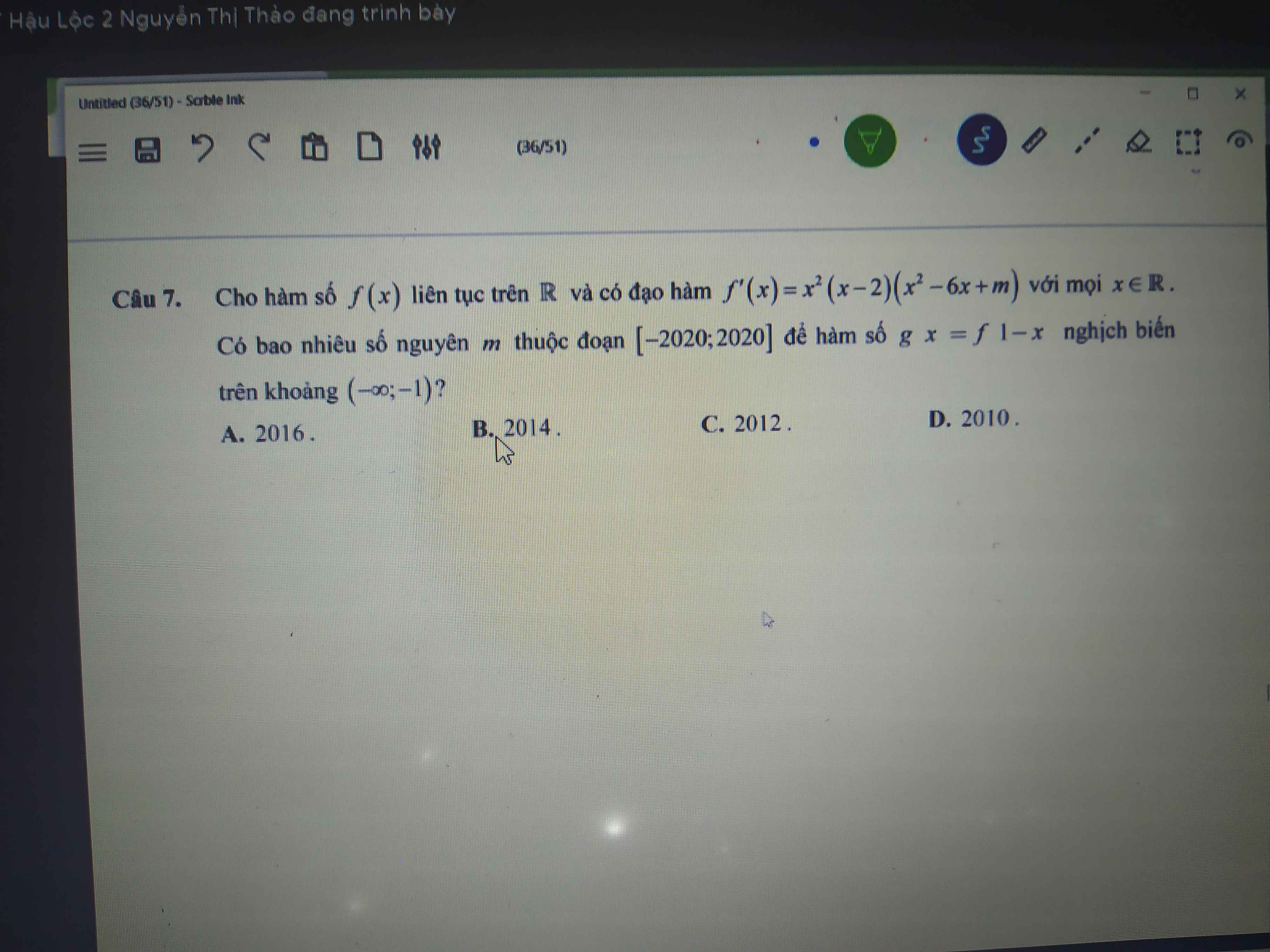
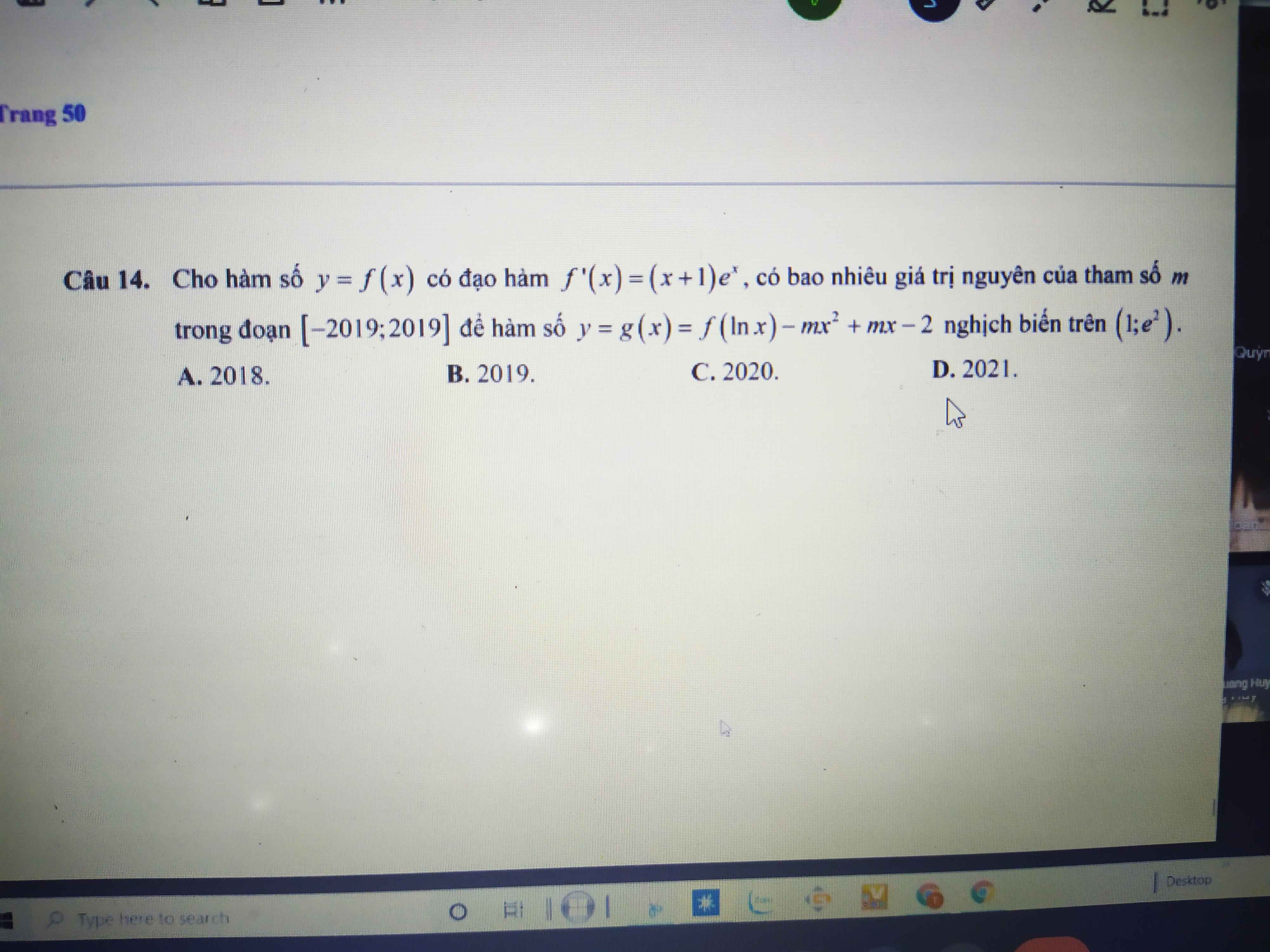
\(g'\left(x\right)=2x\left[f'\left(x^2\right)+m\left(2x^2+4x-6\right)\right]\)

\(\Rightarrow f'\left(x^2\right)+m\left(2x^2+4x-6\right)\le0\) với mọi x thuộc (-3;0) (1)

Từ đồ thị ta thấy \(f'\left(x^2\right)\) luôn âm trên R và \(2x^2+4x-6\) âm trên (-3;0) nên nếu \(m\ge0\Rightarrow g'\left(x\right)< 0\) (thỏa mãn)

Xét với \(m< 0\), tại lân cận của \(x=0\) (nghĩa là tại 1 điểm \(x< 0\) và rất gần 0), ta có:

\(g'\left(x\right)\approx f'\left(0\right)-6m\)

\(-3< f'\left(0\right)< -4\), mà \(m< 0\) và m nguyên \(\Rightarrow-6m\ge6\)

\(\Rightarrow g'\left(x\right)>6-4=2>0\) (không thỏa mãn (1)

\(\Rightarrow m\ge0\Rightarrow B\)