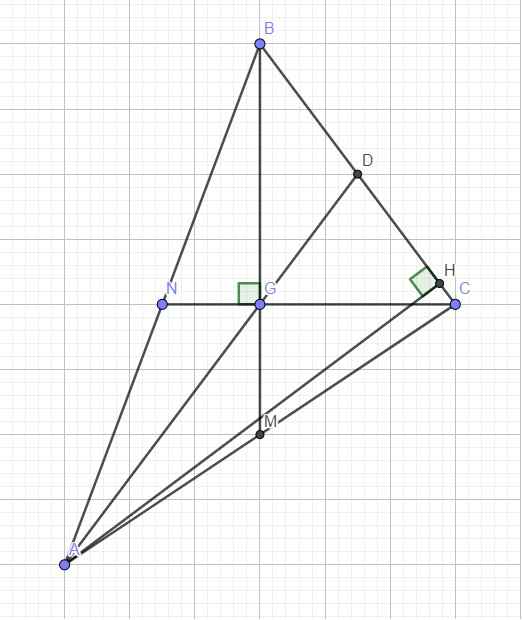
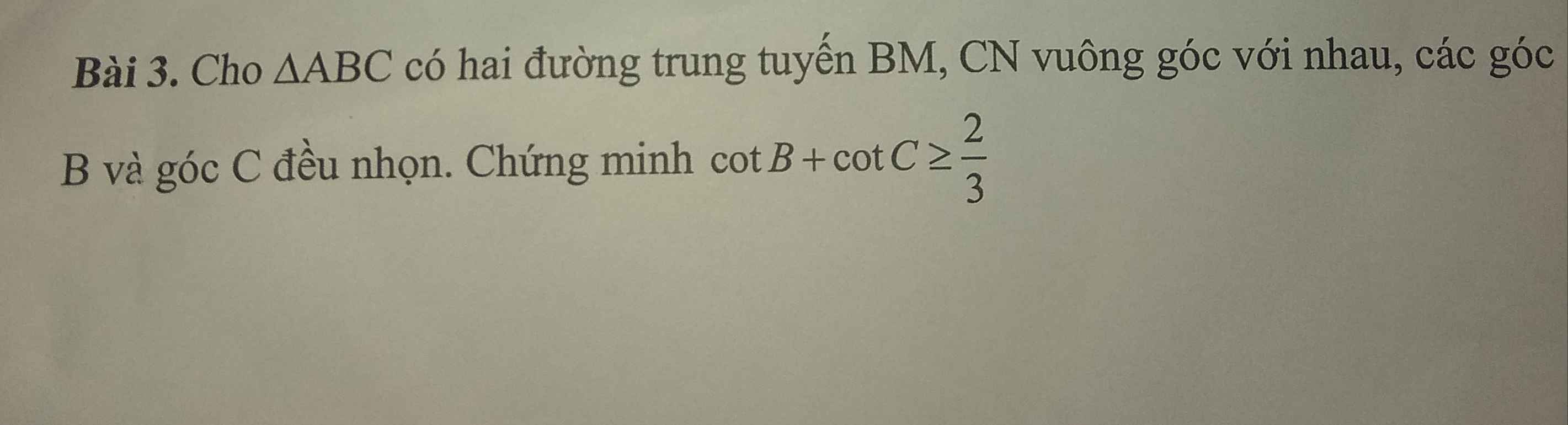Gọi G là giao điểm BM và CN \(\Rightarrow\) G là trọng tâm tam giác ABC
Nối AG cắt BC tại D \(\Rightarrow\) D là trung điểm BC
Trong tam giác vuông BGC, GD là trung tuyến ứng với cạnh huyền
\(\Rightarrow GD=\dfrac{1}{2}BC\) \(\Rightarrow\dfrac{1}{3}AD=\dfrac{1}{2}BC\Rightarrow AD=\dfrac{3}{2}BC\)
Kẻ đường cao AH ứng với BC, do AD là đường xiên và AH là đường vuông góc
\(\Rightarrow AD\ge AH\Rightarrow\dfrac{3}{2}BC\ge AH\Rightarrow BC\ge\dfrac{2}{3}AH\)
Trong tam giác vuông ABH ta có: \(cotB=\dfrac{BH}{AH}\)
Trong tam giác vuông ACH: \(cotC=\dfrac{CH}{AH}\)
\(\Rightarrow cotB+cotC=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BH+CH}{AH}=\dfrac{BC}{AH}\ge\dfrac{\dfrac{2}{3}AH}{AH}=\dfrac{2}{3}\) (đpcm)