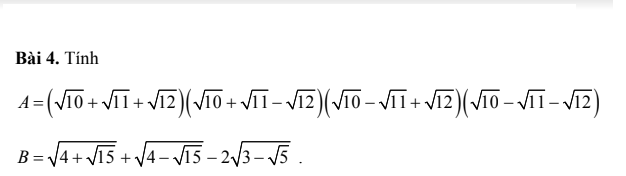Lời giải:
\(A=[(\sqrt{10}+\sqrt{11})^2-(\sqrt{12})^2][(\sqrt{10}-\sqrt{11})^2-(\sqrt{12})^2]\)
\(=(9+2\sqrt{110})(9-2\sqrt{110})=9^2-(2\sqrt{110})^2=81-440=-359\)
\(B=\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)
\(B\sqrt{2}=\sqrt{8+2\sqrt{15}}+\sqrt{8-2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{(\sqrt{5}+\sqrt{3})^2}+\sqrt{(\sqrt{5}-\sqrt{3})^2}-2\sqrt{(\sqrt{5}-1)^2}\)
\(=\sqrt{5}+\sqrt{3}+\sqrt{5}-\sqrt{3}-2(\sqrt{5}-1)=2\)
b) Ta có: \(B=\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}-2\cdot\sqrt{3-\sqrt{5}}\)
\(=\dfrac{\sqrt{8+2\sqrt{15}}+\sqrt{8-2\sqrt{15}}-2\cdot\sqrt{6-2\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}+\sqrt{3}+\sqrt{5}-\sqrt{3}-2\left(\sqrt{5}-1\right)}{\sqrt{2}}\)
\(=\dfrac{2\sqrt{5}-2\sqrt{5}+2}{\sqrt{2}}\)
\(=\sqrt{2}\)