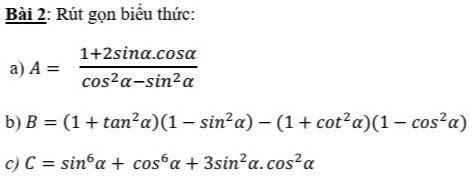\(A=\dfrac{sin^2a+cos^2a+2sinx.cosa}{\left(cosa-sina\right)\left(cosa+sina\right)}=\dfrac{\left(cosa+sina\right)^2}{\left(cosa-sina\right)\left(cosa+sina\right)}=\dfrac{cosa+sina}{cosa-sina}\)
\(B=\left(1+\dfrac{sin^2a}{cos^2a}\right).cos^2a-\left(1+\dfrac{cos^2a}{sin^2a}\right).sin^2a\)
\(=\dfrac{\left(sin^2a+cos^2a\right).cos^2a}{cos^2a}-\dfrac{\left(sin^2a+cos^2a\right).sin^2a}{sin^2a}=1-1=0\)
\(C=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)+3sin^2a.cos^2a\)
\(=1^3-3sin^2a.cos^2a.1+3sin^2a.cos^2a=1\)
Đúng 2
Bình luận (0)
