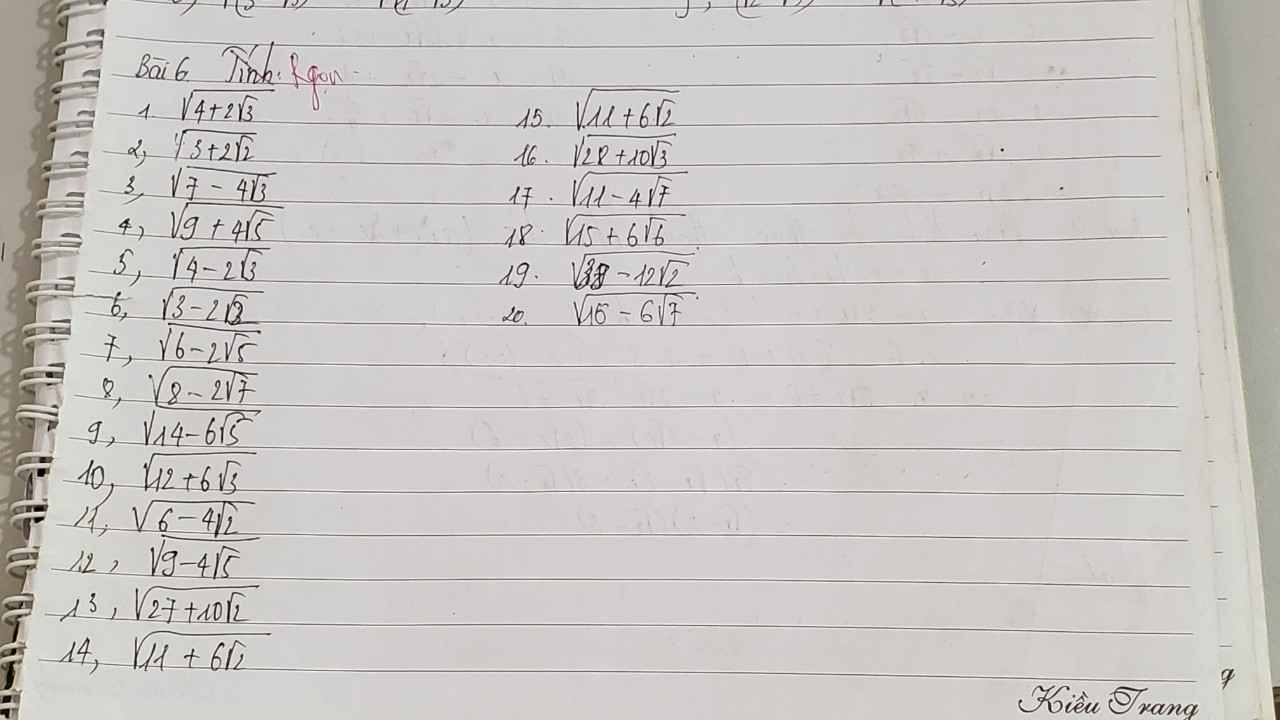Question

Answer 1

1) \(\sqrt{4+2\sqrt{3}}=\sqrt{1^2+2\sqrt{3}+(\sqrt{3})^2}=\sqrt{(1+\sqrt{3})^2}=1+\sqrt{3}\)

2) \(\sqrt{3+2\sqrt{2}}=\sqrt{1^2+2\sqrt{2}+(\sqrt{2})^2}=\sqrt{(1+\sqrt{2})^2}=1+\sqrt{2}\)

3) \(\sqrt{7-4\sqrt{3}}=\sqrt{2^2-4\sqrt{3}+(\sqrt{3})^2}=\sqrt{(2-\sqrt{3})^2}=2-\sqrt{3}\)

4) \(\sqrt{9+4\sqrt{5}}=\sqrt{2^2+4\sqrt{5}+(\sqrt{5})^2}=\sqrt{(2+\sqrt{5})^2}=2+\sqrt{5}\)

Answer 2

9) \(\sqrt{14-6\sqrt{5}}=\sqrt{3^2-2.3.\sqrt{5}+(\sqrt{5})^2}=\sqrt{(3-\sqrt{5})^2}=3-\sqrt{5}\)

10) \(\sqrt{12+6\sqrt{3}}=\sqrt{3^2+2.3.\sqrt{3}+(\sqrt{3})^2}=\sqrt{(3+\sqrt{3})^2}=3+\sqrt{3}\)

11) \(\sqrt{6-4\sqrt{2}}=\sqrt{2^2-2.2.\sqrt{2}+\left(\sqrt{2}\right)^2}=\sqrt{\left(2-\sqrt{2}\right)^2}=2-\sqrt{2}\)

12) \(\sqrt{9-4\sqrt{5}}=\sqrt{2^2-2.2.\sqrt{5}+(\sqrt{5})^2}=\sqrt{(2-\sqrt{5})^2}=2-\sqrt{5}\)

 

Answer 3

5) \(\sqrt{4-2\sqrt{3}}=\sqrt{1^2-2\sqrt{3}+(\sqrt{3})^2}=\sqrt{(1-\sqrt{3})^2}=1-\sqrt{3}\)

6) \(\sqrt{3-2\sqrt{2}}=\sqrt{1^2-2\sqrt{2}+(\sqrt{2})^2}=\sqrt{(1-\sqrt{2})^2}=1-\sqrt{2}\)

7) \(\sqrt{6-2\sqrt{5}}=\sqrt{1^2-2\sqrt{5}+(\sqrt{5})^2}=\sqrt{(1-\sqrt{5})^2}=1-\sqrt{5}\)

8) \(\sqrt{8-2\sqrt{7}}=\sqrt{1^2-2\sqrt{7}+(\sqrt{7})^2}=\sqrt{(1-\sqrt{7})^2}=1-\sqrt{7}\)

Answer 4

13) \(\sqrt{27+10\sqrt{2}}=\sqrt{5^2+2.5\sqrt{2}+(\sqrt{2})^2}=\sqrt{(5+\sqrt{2})^2}=5+\sqrt{2}\)

14,15) \(\sqrt{11+6\sqrt{2}}=\sqrt{3^2+2.3\sqrt{2}+(\sqrt{3})^2}=\sqrt{(3+\sqrt{2})^2}=3+\sqrt{2}\)

16) \(\sqrt{28+10\sqrt{3}}=\sqrt{5^2+2.5.\sqrt{3}+(\sqrt{3})^2}=\sqrt{(5+\sqrt{3})^2}=5+\sqrt{3}\)

17) \(\sqrt{11-4\sqrt{7}}=\sqrt{2^2-2.2.\sqrt{7}+(\sqrt{7})^2}=\sqrt{(2-\sqrt{7})^2}=2-\sqrt{7}\)

Answer 5

18) \(\sqrt{15+6\sqrt{6}}=\sqrt{3^2+2.3.\sqrt{6}+(\sqrt{6})^2}=\sqrt{(3+\sqrt{6})^2}=3+\sqrt{6}\)

19) \(\sqrt{38-12\sqrt{2}}=\sqrt{6^2-2.6.\sqrt{2}+(\sqrt{2})^2}=\sqrt{(6-\sqrt{2})^2}=6-\sqrt{2}\)

20) \(\sqrt{16-6\sqrt{7}}=\sqrt{3^2-2.3.\sqrt{7}+(\sqrt{7})^2}=\sqrt{(3-\sqrt{7})^2}=3-\sqrt{7}\)