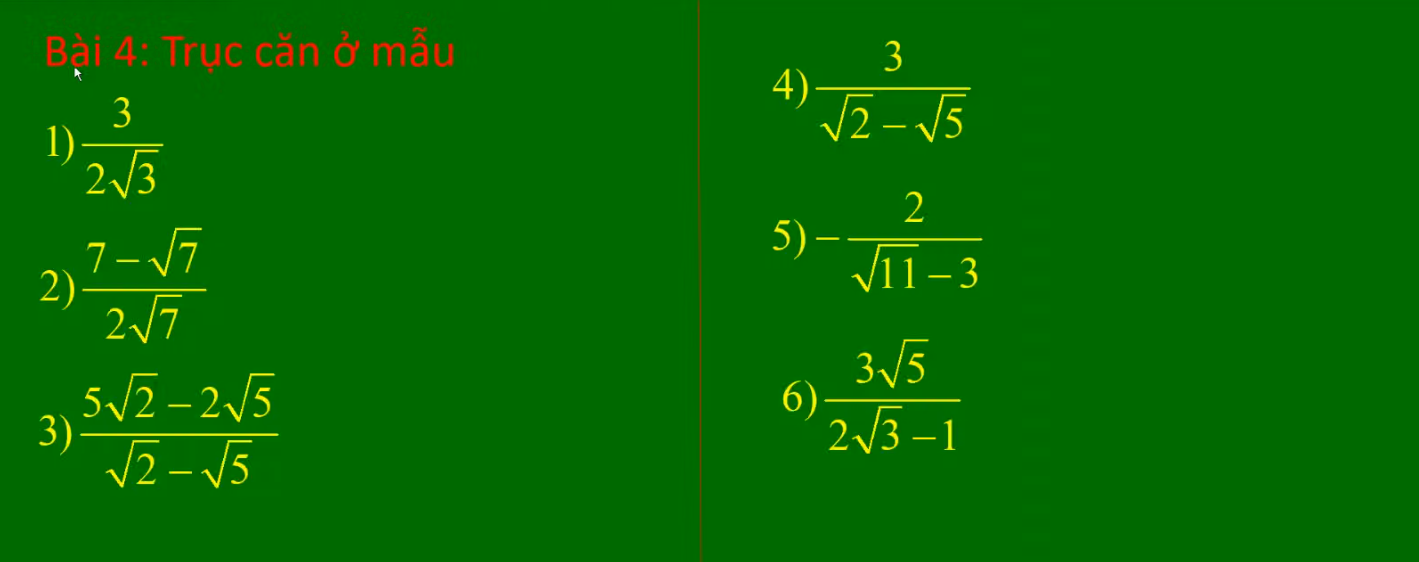\(1.\dfrac{3}{2\sqrt{3}}=\dfrac{\sqrt{3}}{2}\)
\(2.\dfrac{7-\sqrt{7}}{2\sqrt{7}}=\dfrac{7\sqrt{7}-7}{14}=\dfrac{\sqrt{7}-1}{2}\)
\(3.\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}=\dfrac{\sqrt{10}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{2}-\sqrt{5}}=-\sqrt{10}\)
\(4.\dfrac{3}{\sqrt{2}-\sqrt{5}}=-\left(\sqrt{2}+\sqrt{5}\right)\)
\(5.-\dfrac{2}{\sqrt{11}-3}=-\left(\sqrt{11}+3\right)\)
\(6.\dfrac{3\sqrt{5}}{2\sqrt{3}-1}=\dfrac{3\sqrt{5}\left(2\sqrt{3}+1\right)}{12-1}=\dfrac{6\sqrt{15}+3\sqrt{5}}{11}\)
1) \(\dfrac{3}{2\sqrt{3}}=\dfrac{\sqrt{3}.\sqrt{3}}{2\sqrt{3}}=\dfrac{\sqrt{3}}{2}\)
2) \(\dfrac{7-\sqrt{7}}{2\sqrt{7}}=\dfrac{\sqrt{7}\left(\sqrt{7}-1\right)}{2\sqrt{7}}=\dfrac{\sqrt{7}-1}{2}\)
3) \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}=\dfrac{\sqrt{10}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{2}-\sqrt{5}}=-\sqrt{10}\)
4) \(\dfrac{3}{\sqrt{2}-\sqrt{5}}=\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)}=\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{-3}=-\sqrt{2}-\sqrt{5}\)
5) \(-\dfrac{2}{\sqrt{11}-3}=-\dfrac{2\left(\sqrt{11}+3\right)}{\left(\sqrt{11}-3\right)\left(\sqrt{11}+3\right)}=-\dfrac{2\left(\sqrt{11}+3\right)}{2}=-\sqrt{11}-3\)
6) \(\dfrac{3\sqrt{5}}{2\sqrt{3}-1}=\dfrac{3\sqrt{5}\left(2\sqrt{3}+1\right)}{\left(2\sqrt{3}-1\right)\left(2\sqrt{3}+1\right)}=\dfrac{6\sqrt{15}+3\sqrt{5}}{11}\)