Học tại trường
Chưa có thông tin
Đến từ
Đà Nẵng , Chưa có thông tin
Số lượng câu hỏi
1
Số lượng câu trả lời
12
Điểm GP
0
Điểm SP
3
Người theo dõi (9)
Đang theo dõi (21)

Câu trả lời:
1.119909991x1018

Câu trả lời:
TH1 : x=3; y=2
TH2 : x=7; y=4

Câu trả lời:
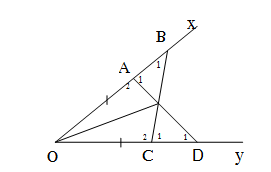
![]() minh ko bik dung sai ahihi
minh ko bik dung sai ahihi![]()
![]()

Câu trả lời:
![]()
con thư 7 chu nhât mà