Question

giải hộ mk bài 43/sgk1/t125 nha( luyện tập về 3 trường hợp bằng nhau của tam giác)

Answer 1

a) ∆OAD và ∆OCB có: OA= OC(gt)

∠O chung

OB = OD (gt)

OAD = OCB (c.g.c) AD = BC

Nên ∆OAD=∆OCB(c.g.c)

suy ra AD=BC.

b)

Ta có ∠A₁ = 180⁰ – ∠A₂

∠C₁ = 180⁰ – ∠C₂

mµ ∠A₂ = ∠C₂ do ΔOAD = ΔOCB (c/m trên)

⇒ ∠A₁ = ∠C₁

Ta có OB = OA + AB

OD = OC + CD mà OB = OD, OA = OC ⇒ AB = CD

Xét ΔEAB = ΔECD có:

∠A₁ = ∠C₁ (c/m trên)

AB = CD (c/m trên)

∠B₁ = ∠D₁ (ΔOCB = ΔOAD)

⇒ ΔEAB = ΔECD (g.c.g)

c) Xét ΔOBE và ΔODE có:

OB = OD (GT)

OE chung

AE = CE (ΔAEB = ΔCED) ⇒ΔOBE = ΔODE (c.c.c)

⇒ ∠AOE = ∠COE ⇒ OE là phân giác của góc ∠xOy.

Answer 2

Answer 3

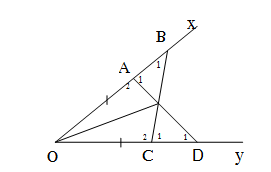
Bài 43. Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA<OB.

Lấy các điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC.

Chứng minh rằng:

a) AD=BC;

b) ∆EAB=∆ECD;

c )OE là tia phân giác của xOy.

Answer 4

​minh ko bik dung sai ahihi