Học tại trường
Chưa có thông tin
Đến từ
Hải Phòng , Chưa có thông tin
Số lượng câu hỏi
11
Số lượng câu trả lời
478
Điểm GP
122
Điểm SP
554














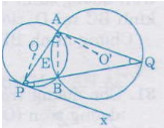
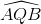 =
= 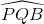 (1)
(1) sđ
sđ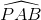 =
= 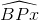 (2)
(2)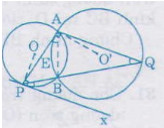
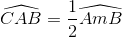 (1)
(1)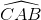 là góc tạo bởi một tiếp tuyến và một dây cung đi qua tiếp điểm A của (O')).
là góc tạo bởi một tiếp tuyến và một dây cung đi qua tiếp điểm A của (O')).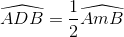 (2)
(2)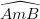
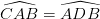 (3)
(3)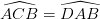 (4)
(4)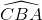 =
=