Học tại trường
Chưa có thông tin
Đến từ
Vĩnh Long , Chưa có thông tin
Số lượng câu hỏi
0
Số lượng câu trả lời
350
Điểm GP
84
Điểm SP
690














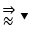 xong trong đó có dấu thuộc thì bn chọn
xong trong đó có dấu thuộc thì bn chọn