Tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+2}{x+1}\) là:
A. x = – 1. B. x = – 2. C. x = 1. D. x = 2.
Bài 3: Đường tiệm cận của đồ thị hàm số
Bài tập 1 (SGK Cánh Diều - Tập 1 - Trang 27)
Thảo luận (1)
Bài tập 2 (SGK Cánh Diều - Tập 1 - Trang 27)
Tiệm cận xiên của đồ thị hàm số \(y=\dfrac{x^2+3x+5}{x+2}\) là:
A. y = x. B. y = x + 1. C. y = x + 2. D. y = x + 3.
Thảo luận (1)Hướng dẫn giảiTa có: \(y = \frac{{{x^2} + 3x + 5}}{{x + 2}} = x + 1 + \frac{3}{{x + 2}}\)
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\)
Vậy đường thẳng \(y = x + 1\) là đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x + 5}}{{x + 2}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 2 (SGK Cánh Diều - Tập 1 - Trang 23)
Tìm tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2+3x}{x-5}\).
Thảo luận (1)Hướng dẫn giảiTập xác định \(D = \mathbb{R}\backslash \left\{ 5 \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \frac{{{x^2} + 3x}}{{x - 5}} = - \infty \\\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \frac{{{x^2} + 3x}}{{x - 5}} = + \infty \end{array} \right.\)
Vậy đường thẳng \(x = 5\) là tiệm cận đứng của đồ thị hàm số đã cho
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 4 (SGK Cánh Diều - Tập 1 - Trang 26)
Tìm tiệm cận xiên của đồ thị hàm số
\(y=f\left(x\right)=\dfrac{x^2-3x+2}{x+3}.\)
Thảo luận (1)Hướng dẫn giảiTa có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 3 (SGK Cánh Diều - Tập 1 - Trang 24)
Cho hàm số yfleft(xright)x+1+dfrac{1}{x-1} có đồ thị (C) và đường thẳng y x + 1 (Hình 15).Tìm limlimits_{xrightarrow+infty}left[fleft(xright)-left(x+1right)right];limlimits_{xrightarrow-infty}left[fleft(xright)-left(x+1right)right].
Đọc tiếp
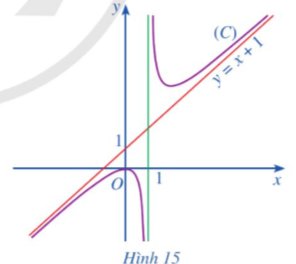
Cho hàm số \(y=f\left(x\right)=x+1+\dfrac{1}{x-1}\) có đồ thị (C) và đường thẳng y = x + 1 (Hình 15).
Tìm \(\lim\limits_{x\rightarrow+\infty}\left[f\left(x\right)-\left(x+1\right)\right];\lim\limits_{x\rightarrow-\infty}\left[f\left(x\right)-\left(x+1\right)\right]\).
Thảo luận (1)Hướng dẫn giảiTa có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 2 (SGK Cánh Diều - Tập 1 - Trang 22)
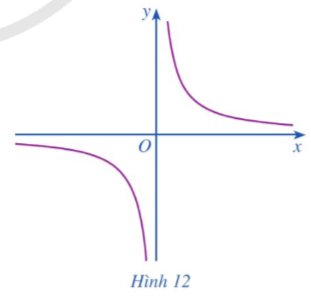
Cho hàm số \(y=f\left(x\right)=\dfrac{1}{x}\) có đồ thị là đường cong như Hình 12.
Tìm \(\lim\limits_{x\rightarrow0^+}f\left(x\right),\lim\limits_{x\rightarrow0^-}f\left(x\right).\)
Thảo luận (1)Hướng dẫn giảiTa có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - \infty \).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 1 (SGK Cánh Diều - Tập 1 - Trang 21)
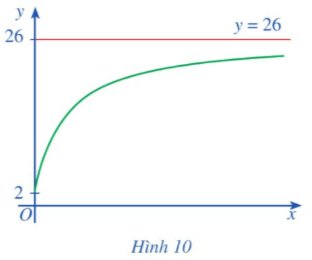
Xét hàm số \(y=f\left(x\right)=\dfrac{26x+10}{x+5}\) , với x ∈ [0; + \(\infty\)) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)\).
Thảo luận (1)Hướng dẫn giảiTa có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 26\)
(Trả lời bởi Nguyễn Quốc Đạt)
Khởi động (SGK Cánh Diều - Tập 1 - Trang 21)
Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thứcyfleft(xright)dfrac{26x+10}{x+5}(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y f(x) là một hàm số xác định trên nửa khoảng [0; + infty), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.Khi xrightarrow+infty, đồ thị hàm số y f(x) ngày càng “tiến gần” tới đường thẳng nào?
Đọc tiếp
Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức
\(y=f\left(x\right)=\dfrac{26x+10}{x+5}\)
(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + \(\infty\)), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.
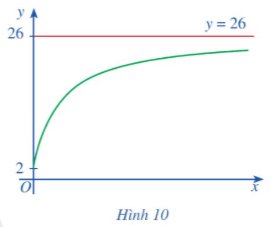
Khi \(x\rightarrow+\infty\), đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?
Thảo luận (1)Hướng dẫn giảiKhi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng y = 26.
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 1 (SGK Cánh Diều - Tập 1 - Trang 22)
Tìm tiệm cận ngang của đồ thị hàm số \(y=\dfrac{3x-2}{x+1}\).
Thảo luận (1)Hướng dẫn giảiTập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = 3\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\end{array} \right.\).
Vậy đường thẳng \(y = 3\) là tiệm cận ngang của đồ thị hàm số đã cho
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 3 (SGK Cánh Diều - Tập 1 - Trang 25)
Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số
\(y=f\left(x\right)=\dfrac{-x^2-2x+3}{x+2}\).
Thảo luận (1)Hướng dẫn giảiTa có: \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} = - x + \frac{3}{{x + 2}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\).
Vậy đường thẳng \(y = - x\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\)
(Trả lời bởi Nguyễn Quốc Đạt)