Bài 1: Hàm số lượng giác

1) điều điện : \(\begin{cases}1+cos3x\ge0\\sin2x\ne0\\1-cos4x\ne0\end{cases}\)

+) sin2x \(\ne\)0 => x \(\ne\) \(\frac{k\pi}{2}\) với k thuộc Z

+) 1-cos4x \(\ne\)0=> cos4x\(\ne\)1=> x\(\ne\)\(\frac{k\pi}{2}\) với k thuộc Z

+) 1+cos3x \(\ge\)0=> cos3x\(\ge\)-1=> x\(\ge\)\(\frac{\pi}{3}+\frac{k2\pi}{3}\) với k thuộc Z

hợp 3 cái trên là xong

2) điều kiện : tanx, cos2x\(\ne\)0

+) tanx \(\ne\)0 <=> x \(\ne\frac{\pi}{2}+k\pi\) k thuộc Z

+) cos2x \(\ne\)0 <=> x\(\ne\frac{\pi}{4}+\frac{k\pi}{2}\) với k thuộc Z

hợp 2 cái vào là được

ta có -1\(\le cosx\le1\)

=> GTLN A=3.1+1=4

=> GTNN: A= -1.3+1=-2

Ta có: \(-1\le\cos x\le1\)

\(\Rightarrow y_{max}=3.1+1=4(cm) \) khi \(\cos(x)=1\leftrightarrow x=k2\pi\)

\(y_{mim}=3.(-1)+1=-2(cm) \) khi \(\cos(x)=-1\leftrightarrow x=\pi +k2\pi\)

ta có -1\(\le sin4x\le1\)

=> y_min=2.-1+3=1

GTNN y=1 khi x\(=\frac{-\pi}{8}+\frac{k2\pi}{ }\)với k thuộc Z

=> y_max= 2.1+3=5

GTLN y=5 khi x=\(\frac{\pi}{8}+\frac{k\pi}{2}\) với k thuộc Z

 a) cosx - √3sinx = √2 ⇔ cosx - tansinx = √2

         ⇔ coscosx - sinsinx = √2cos  ⇔ cos(x + ) = 

         ⇔  

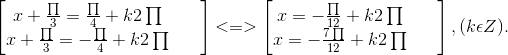
         b) 3sin3x - 4cos3x = 5 ⇔ sin3x - cos3x = 1.

         Đặt α = arccos thì phương trình trở thành

         cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α =  + k2π

         ⇔ x =  , k ∈ Z (trong đó α = arccos).

         c) Ta có sinx + cosx =  √2cos(x - ) nên phương trình tương đương với

          2√2cos(x - ) - √2 = 0 ⇔ cos(x - ) = 

          ⇔  

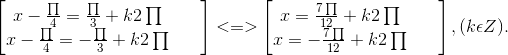
         d) 5cos2x + 12sin2x -13 = 0 ⇔ 

         Đặt α = arccos thì phương trình trở thành

            cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1

         ⇔ x =  + kπ, k ∈ Z (trong đó α = arccos).

Dương Hoàng Minh làm kiểu j mà 1 nấy bài trong 2p ?