Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là :
a) Hình chữ nhật ?
b) Hình thoi
c) Hình vuông ?
Ôn tập chương I : Tứ giác
Bài 88 (Sgk tập 1 - trang 111)
Thảo luận (3)
Bài 89 (Sgk tập 1 - trang 111)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D
a) Chứng minh rằng điểm E đối xứng với M qua AB
b) Các tứ giác AEMC, AEBM là hình gì ? Vì sao ?
c) Cho BC = 4cm, tính chu vi tứ giác AEBM
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông ?
Thảo luận (3)Hướng dẫn giảia) Ta có: E và M đối xứng với nhau qua D
(Trả lời bởi Hương Yangg)
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trung điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC;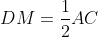
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành
Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành
mà AB vuông góc EM
=> AEBM là hình thoi
c, Ta có : AM =( trung tuyến ứng với cạnh huyền)
=> AM =(cm)
Chu vi hình thoi AEBM:
2 . 4 =8 (cm)
d, Nếu AEBM là hình vuông
thì= góc B= góc M= 90 độ
<=> AM vuông góc BC
<=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
<=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông
Bài 90 (Sgk tập 1 - trang 112)
Đố :
Tìm trục đối xứng và tâm đối xứng của :
a) Hình 110 (sơ đồ một sân quần vợt)
b) Hình 111
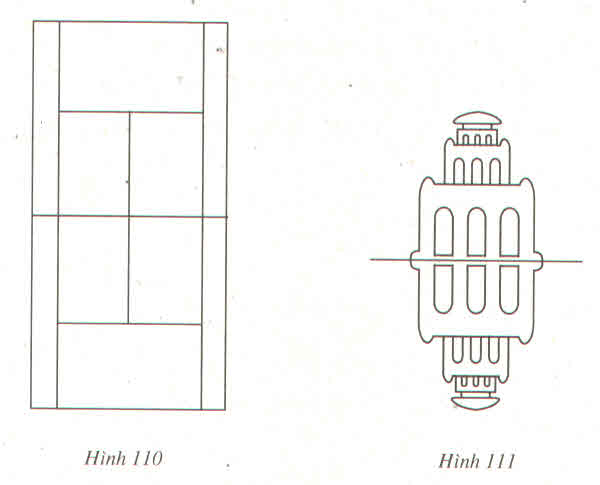
Thảo luận (3)Hướng dẫn giảia) Hình 110 (sân quần vợt) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng AB và CD.
-Một tâm đối xứng là O.
b) Hình 111 (Tháp Rùa và bóng của nó trên mặt nước) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng là MN và PQ.
- Một tâm đối xứng là I.
(Trả lời bởi Hương Yangg)
Bài 157 (Sách bài tập - trang 99)
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là :
a) Hình chữ nhật
b) Hình thoi
c) Hình vuông
Thảo luận (2)Hướng dẫn giảiCái hình hơi khó vẽ! :(
Giải:
Ta có: \(EA=EB,FB=FC\left(gt\right)\)
\(\Rightarrow EF\) là đường trung bình của \(\Delta BAC\)
\(\Rightarrow\) \(EF//AC\) và \(EF=\dfrac{AC}{2}\left(1\right)\)
Chứng minh tương tự ta có:
\(HG//AC\) và \(HC=\dfrac{AC}{2}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra: \(EF//GH\) và \(EF=GH\)
\(\Rightarrow EFGH\) là hình bình hành
a) Hình bình hành \(EFGH\) là hình chữ nhật
\(\Leftrightarrow\widehat{FEH}=90^0\Leftrightarrow EF\perp EH\Leftrightarrow AC\perp BD\)\((EF//AC,EH//BD)\)
b) Hình bình hành \(EFGH\) là hình thoi
\(\Leftrightarrow EF=EH\Leftrightarrow AC=BD\) \(\left(EF=\dfrac{AC}{2};EH=\dfrac{BD}{2}\right)\)
c) Hình bình hành \(EFGH\) là hình vuông \(\Leftrightarrow\left\{{}\begin{matrix}AC\perp BD\\AC=BD\end{matrix}\right.\)
(Trả lời bởi Hoang Hung Quan)
Bài 158 (Sách bài tập - trang 100)
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?
c) Chứng minh rằng M đối xứng với N qua A
d) Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?
Đọc tiếp
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?
c) Chứng minh rằng M đối xứng với N qua A
d) Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?
Thảo luận (1)Hướng dẫn giải
Bài 159 (Sách bài tập - trang 100)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC
a) Chứng minh rằng D đối xứng với E qua A
b) Tam giác DHE là tam giác gì ? Vì sao ?
c) Tứ giác BDEC là hình gì ? Vì sao ?
d) Chứng minh rằng BC = BD + CE
Thảo luận (1)Hướng dẫn giải
a) AB là đường trung trực của HD \(\Rightarrow\) AD = AH.
AC là đường trung trực của HE \(\Rightarrow\) AE = AH.
Suy ra AD = AE. (1)
Tam giác AHD cân nên \(\widehat{HAD}=2\widehat{A_1}.\)
Tam giác AHE cân nên \(\widehat{HAE}=2\widehat{A_2}.\)
Suy ra \(\widehat{HAD}+\widehat{HAE}=2\widehat{A_1}+2\widehat{A_2}=2\left(\widehat{A_1}+\widehat{A_2}\right)\)
\(\widehat{HAD}+\widehat{HAE}=2.90^o=180^o.\)
Do đó D, A, E thẳng hàng. (2)
Từ (1) và (2) suy ra A là trung điểm của DE. Vậy D đối xứng với E qua A.
b) Tam giác DHE có HA là đường trung tuyến và HA = \(\dfrac{1}{2}\) DE nên \(\Delta DHE\) vuông tại H.
c) Hãy chứng minh \(\widehat{ADB}=\widehat{AHB}=90^o,\widehat{AEC}=90^o\) để suy ra BDEC là hình thang vuông
d) Hãy chứng minh BD = BH, CE = CH.
(Trả lời bởi Hải Ngân)
Bài 160 (Sách bài tập - trang 100)
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là :
a) Hình chữ nhật
b) Hình thoi
c) Hình vuông
Thảo luận (2)Hướng dẫn giải
Bài 161 (Sách bài tập - trang 100)
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC
a) Chứng minh rằng tứ giác DEHK là hình bình hành
b) Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật
c) Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì ?
Thảo luận (3)Hướng dẫn giải
Bài 162 (Sách bài tập - trang 100)
Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.
a) Các tứ giác AEFD, AECF là hình gì ? Vì sao ?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật ?
c) Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông ?
Thảo luận (2)Hướng dẫn giải
a) Tứ giác AEFD là hình thoi, tứ giác AECF là hình bình hành (tự chứng minh).
b) Tứ giác AECF là hình bình hành nên EN // FM. Tứ giác AECF là hình bình hành nên EM // FN. AEFD là hình thoi nên AF \(\perp\) DE.
Hình bình hành EMFN có \(\widehat{M}=90^o\) nên là hình chữ nhật.
c) Hình chữ nhật EMFN là hình vuông
\(\Leftrightarrow\) ME = MF \(\Leftrightarrow\) DE = AF (vì DE = 2ME, AF = 2MF)
\(\Leftrightarrow\) Hình thoi AEFD có hai đường chéo bằng nhau
\(\Leftrightarrow\) AEFD là hình vuông \(\Leftrightarrow\) \(\widehat{A}=90^o\).
\(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.
Như vậy, hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật.
(Trả lời bởi Hải Ngân)
Bài 163 (Sách bài tập - trang 100)
Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD
a) Tứ giác DEBF là hình gì ? Vì sao ?
b) Chứng minh rằng các đường thẳng AC, BD, EF cùng cắt nhau tại một điểm
c) Gọi giao điểm của AC với DE và BF theo thứ tứ là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành
Thảo luận (2)Hướng dẫn giải
a) Trong tứ giác DEBF có:
Hai đường chéo BD và EF cắt nhau tại trung điểm O
Các cạnh đối BE và DF bằng nhau
\(\Rightarrow\) Tứ giác DEBF là hình bình hành.
b) Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, ta có O là trung điểm của BD.
Theo câu a), DEBF là hình bình hành nên trung điểm O của BD cũng là trung điểm của EF.
Vậy AC, BD, EF cùng cắt nhau tại điểm O.
c) \(\Delta ABD\) có các đường trung tuyến AO, DE cắt nhau ở M nên OM = \(\dfrac{1}{3}\) OA.
\(\Delta CBD\) có các đường trung tuyến CO, BF cắt nhau ở N nên ON = \(\dfrac{1}{3}\) OC.
Tứ giác EMFN có các đường chéo cắt nhau tại trung điểm của mỗi đường OM = ON, OE = OF nên là hình bình hành.
(Trả lời bởi Hải Ngân)