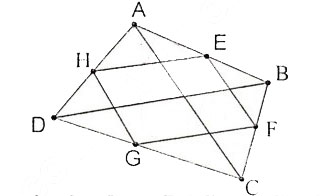
Ta có : HE, GF lần lượt là đường trung bình của tam giác ADB và tam giác CDB
=> HE // BD, GF // BD và BD = 2HE = 2GF
Tương tự : HG, EF lần lượt là đường trung bình của tam giác DAC và tam giác BAC
=> HG // AC, EF // AC và AC = 2HG = 2EF
Nên EFGH là hình bình hành.
a) Đề hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF => BD ⊥ AC
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF => BD = AC
Điều kiện phải tìm : Hai đường chéo AC và BD bằng nhau.
c) Để hình bình hành EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật, vừa là hình thoi => BD ⊥ AC và BD = AC.
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau và bằng nhau.
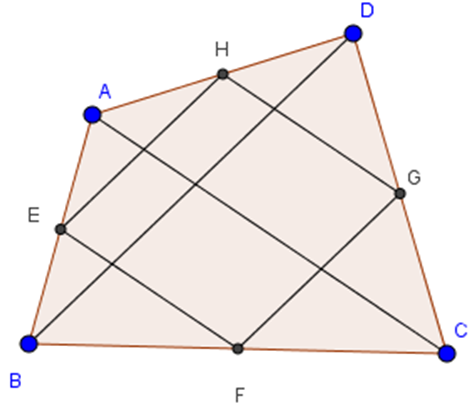
Ta có: HE, GF lần lượt là đường trung bình của ΔADB và Δ CDB
⇒ HE//BD, GF//BD và HE = GF = BD/2
Tương tự: HG, EF lần lượt là đường trung bình của ΔDAC và ΔBAC
⇒ HG//AC, EF //AC và HG = EF = AC/2
⇒ Tứ giác EFGH là hình bình hành.
a) Để hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF ⇒ BD ⊥ AC
Điều kiện phải tìm là: Hai đường chéo AC và BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF ⇒ BD = AC
Điều kiện phải tìm là: Hai đường chéo AC và BD bằng nhau
c) Để hình bình hành EFGH là hình vuông thì EFGH vừa là hình chữ nhật, vừa hình thoi. Suy ra BD ⊥ AC và BD = AC
Điều kiện phải tìm là: Hai đường chéo AC và BD vuông góc với nhau và bằng nhau.