Chứng minh:
a. Nếu \(a > 5\) thì \(\frac{{a - 1}}{2} - 2 > 0\).
b. Nếu \(b > 7\) thì \(4 - \frac{{b + 3}}{5} < 2\).
Chứng minh:
a. Nếu \(a > 5\) thì \(\frac{{a - 1}}{2} - 2 > 0\).
b. Nếu \(b > 7\) thì \(4 - \frac{{b + 3}}{5} < 2\).
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a. Bất phương trình \(ax + b < 0\) với \(a > 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
b. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
c. Bất phương trình \(ax + b < 0\) với \(a < 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).
d. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).
Thảo luận (1)Hướng dẫn giải
Giải các bất phương trình:
a. \(5 + 7x \le 11\);
b. \(2,5x - 6 > 9 + 4x\);
c. \(2x - \frac{{x - 7}}{3} < 9\);
d. \(\frac{{3x + 5}}{2} + \frac{x}{5} - 0,2x \ge 4\).
Thảo luận (1)Hướng dẫn giảia.
\(\begin{array}{l}5 + 7x \le 11\\7x \le 6\\x \le \frac{6}{7}\end{array}\)
Vậy nghiệm của bất phương trình là \(x \le \frac{6}{7}\).
b.
\(\begin{array}{l}2,5x - 6 > 9 + 4x\\2,5x - 4x > 9 + 6\\ - 1,5x > 15\\x < - 10\end{array}\)
Vậy nghiệm của bất phương trình là \(x < - 10\).
c.
\(\begin{array}{l}2x - \frac{{x - 7}}{3} < 9\\\frac{{6x}}{3} - \frac{{x - 7}}{3} < \frac{{27}}{3}\\6x - x + 7 - 27 < 0\\5x - 20 < 0\\5x < 20\\x < 4\end{array}\)
Vậy nghiệm của bất phương trình là \(x < 4\).
d.
\(\begin{array}{l}\frac{{3x + 5}}{2} + \frac{x}{5} - 0,2x \ge 4\\\frac{{5\left( {3x + 5} \right)}}{{10}} + \frac{{2x}}{{10}} - \frac{{2x}}{{10}} \ge \frac{{40}}{{10}}\\15x + 25 + 2x - 2x - 40 \ge 0\\15x - 15 \ge 0\\15x \ge 15\\x \ge 1\end{array}\)
Vậy nghiệm của bất phương trình là \(x \ge 1\).
(Trả lời bởi Hà Quang Minh)
Cho \(4,2 < a < 4,3\). Chứng minh: \(13,8 < 3a + 1,2 < 14,1\).
Thảo luận (1)Hướng dẫn giảiDo: \(4,2 < a < 4,3\) nên \(12,6 < 3a < 12,9\). Vậy \(13,8 < 3a + 1,2 < 14,1\).
(Trả lời bởi Hà Quang Minh)
Chứng minh nửa chu vi của một tam giác lớn hơn độ dài mỗi cạnh của tam giác đó.
Thảo luận (1)Hướng dẫn giảiGọi ba cạnh của tam giác lần lượt là a, b, c.
Áp dụng bất đẳng thức tam giác ta có \(a + b > c\) nên \(a + b + c > 2c\). Vậy \(\frac{{a + b + c}}{2} > c\).
Áp dụng bất đẳng thức tam giác ta có \(a + c > b\) nên \(a + b + c > 2b\). Vậy \(\frac{{a + b + c}}{2} > b\).
Áp dụng bất đẳng thức tam giác ta có \(b + c > a\) nên \(a + b + c > 2a\). Vậy \(\frac{{a + b + c}}{2} > a\).
Vậy nửa chu vi của tam giác lớn hơn mỗi cạnh của tam giác đó.
(Trả lời bởi Hà Quang Minh)
Để đổi từ độ Fahrenheit (Độ F) sang độ Celsius (Độ C), người ta dùng công thức sau: \(C = \frac{5}{9}\left( {F - 32} \right)\).
a. Giả sử nhiệt độ ngoài trời của một ngày mùa hè ít nhất là \(95^\circ F\). Hỏi nhiệt độ ngoài trời khi đó ít nhất là bao nhiêu độ C?
b. Giả sử nhiệt độ ngoài trời của một ngày mùa hè ít nhất là \(36^\circ C\). Hỏi nhiệt độ ngoài trời khi đó ít nhất là bao nhiêu độ F?
Thảo luận (1)Hướng dẫn giảia. Nhiệt độ ngoài trời khi đó ít nhất là:
\(\begin{array}{l}C \ge \frac{5}{9}\left( {95 - 32} \right)\\C \ge \frac{5}{9}.63\\C \ge 35\end{array}\)
Vậy nhiệt độ ngoài trời khi đó ít nhất là 35 độ C.
b. Nhiệt độ ngoài trời khi đó ít nhất là:
\(\begin{array}{l}36 \le \frac{5}{9}\left( {F - 32} \right)\\64,8 \le F - 32\\F \ge 96,8\end{array}\)
Vậy nhiệt độ ngoài trời khi đó ít nhất là \(97\) độ F.
(Trả lời bởi Hà Quang Minh)
Đến ngày 31/12/2022, gia đình bác Hoa đã tiết kiệm được số tiền là 250 triệu đồng. Sau thời điểm đó, mỗi tháng gia đình bác Hoa đều tiết kiệm được 10 triệu đồng. Gia đình bác Hoa dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá tối thiểu là 370 triệu đồng. Hỏi sau ít nhất bao nhiêu tháng gia đình bác Hoa có thể mua được chiếc ô tô đó bằng số tiền tiết kiệm được?
Thảo luận (1)Hướng dẫn giảiGọi số tháng bác Hoa có thể mua được chiếc ô tô bằng số tiền tiết kiệm là \(x\) (tháng, \(x \in {\mathbb{N}^*}\))
Số tiền \(x\) tháng bác Hoa tiết kiệm được là \(10x\) (triệu đồng).
Do gia đình bác Hoa dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá tối thiểu là 370 triệu đồng nên ta có:
\(10x + 250 \ge 370\)
Giải bất phương trình trên, ta có:
\(\begin{array}{l}10x + 250 \ge 370\\10x \ge 120\\x \ge 12\end{array}\)
Vậy sau ít nhất 12 tháng gia đình bác Hoa có thể mua được chiếc ô tô đó bằng số tiền tiết kiệm.
(Trả lời bởi Hà Quang Minh)
Chỉ số khối cơ thể, thường được biết đến với tên viết tắt BMI (tiếng Anh là Body Mass Index) cho phép đánh giá thể trạng của một người là gầy, bình thường hay béo. Chỉ số khối cơ thể của một người được tính theo công thức sau: \(BMI = \frac{m}{{h{}^2}}\), trong đó m là khố lượng cơ thể tính theo kilôgam, h là chiều cao tính theo mét.
Dưới đây là bảng đánh giá thể trạng ở người lớn theo BMI đối với khu vực châu Á – Thái Bình Dương:
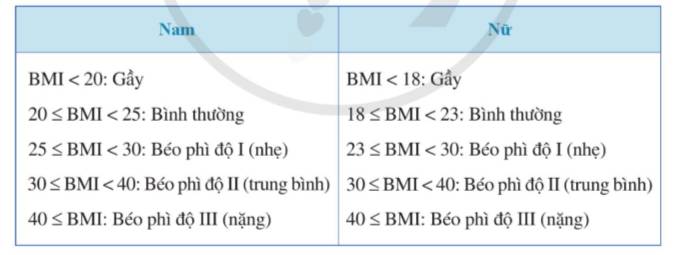
a. Giả sử một người đàn ông có chiều cao 1,68m. Hãy lập bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng trên.
b. Giả sử một người phụ nữ có chiều cao 1,6m. Hãy lập bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng trên.
Thảo luận (1)Hướng dẫn giải
Một nhà máy sản xuất xi măng mỗi ngày đều sản xuất được 100 tấn xi măng. Lượng xi măng tồn trong kho của nhà máy là 300 tấn. Hỏi nhà máy đó cần ít nhất bao nhiêu ngày để có thể xuất đi 15 300 tấn xi măng (tính cả lượng tồn trong kho)?
Thảo luận (1)Hướng dẫn giảiGọi số ngày ít nhất nhà máy sản xuất 15 300 tấn xi măng là \(x\) (ngày, \(x \in {\mathbb{N}^*}\))
Số tấn xi măng \(x\) ngày, nhà máy sản xuất được: \(100x\) (tấn)
Do nhà máy cần xuất 15 300 tấn xi măng (tính cả lượng tồn trong kho) nên ta có
\(100x + 300 \ge 15300\)
Giải bất phương trình trên, ta có:
\(\begin{array}{l}100x + 300 \ge 15300\\100x \ge 15000\\x \ge 150\end{array}\)
Vậy nhà máy cần ít nhất 150 ngày để có thể xuất đi 15 300 tấn xi măng.
(Trả lời bởi Hà Quang Minh)
Cho \(a \ge 2\). Chứng minh:
a. \({a^2} \ge 2a\)
b. \({\left( {a + 1} \right)^2} \ge 4a + 1\)
Thảo luận (1)Hướng dẫn giảiDo \(a \ge 2\) nên \(a - 2 \ge 0\).
a. Xét hiệu: \({a^2} - 2a = a\left( {a - 2} \right) \ge 0\).
Vậy \({a^2} \ge 2a\).
b. Xét hiệu: \({\left( {a + 1} \right)^2} - \left( {4a + 1} \right)\) \( = {a^2} + 2a + 1 - 4a - 1 \) \(= {a^2} - 2a \) \(= a\left( {a - 2} \right) \ge 0\).
Vậy \({\left( {a + 1} \right)^2} \ge 4a + 1\).
(Trả lời bởi Hà Quang Minh)