Trên hình 8, cho ABCD là hình bình hành.
Chứng minh rằng AECF là hình bình hành ?
Bài 7: Hình bình hành
Bài 76 (Sách bài tập - trang 89)
Thảo luận (1)
Bài 77 (Sách bài tập - trang 89)
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Thảo luận (2)Hướng dẫn giải
Bài 78 (Sách bài tập - trang 89)
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB ?
Thảo luận (1)Hướng dẫn giải
Bài 79 (Sách bài tập - trang 89)
Tính các góc của hình bình hành ABCD, biết :
a) \(\widehat{A}=110^0\)
b) \(\widehat{A}-\widehat{B}=20^0\)
Thảo luận (1)Hướng dẫn giảia) \(\widehat{A}=\widehat{C}=110^0;\widehat{B}=\widehat{D}=70^0\)
b) \(\widehat{A}=\widehat{C}=100^0;\widehat{B}=\widehat{D}=80^0\)
(Trả lời bởi Nguyen Thuy Hoa)
Bài 80 (Sách bài tập - trang 89)
Trong tứ giác ở hình 9, tứ giác nào là hình bình hành ?
Thảo luận (2)Hướng dẫn giảiTứ giác ABCD là hình bình hành vì hai cạnh đối AD, BC song song và bằng nhau.
Tứ giác IKMN là hình bình hành vì KM // IN, IK // MN (hoặc vì \(\widehat{I}=\widehat{M},\widehat{K}=\widehat{N}\) )
(Trả lời bởi Nguyen Thuy Hoa)
Bài 81 (Sách bài tập - trang 90)
Chu vi hình bình hành ABCD bằng 10 cm, chu vu tam giác ABD bằng 9cm. Tính độ dài BD ?
Thảo luận (1)Hướng dẫn giải
Bài 82 (Sách bài tập - trang 90)
Hình 10
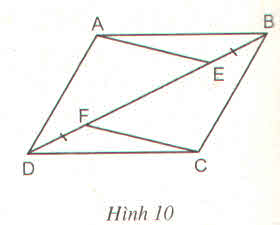
Cho ABCD là hình bình hành. Chứng minh rằng AE // CF ?
Thảo luận (3)Hướng dẫn giảiGọi O là giao điểm của AC và BD. Ta có OA = OC, OE = OF nên AECF là hình bình hành. Suy ra AE // CF.
(Trả lời bởi Nguyen Thuy Hoa)
Bài 83 (Sách bài tập - trang 90)
Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE. N là giao điểm của BF và CE. Chứng minh rằng :
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
Thảo luận (2)Hướng dẫn giải
Bài 84 (Sách bài tập - trang 90)
Trên hình 11, cho ABCD là hình bình hành.
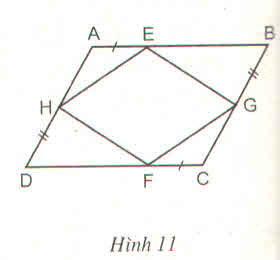
Chứng minh rằng :
a) EGFH là hình bình hành
b) Các đường thẳng AC, BD, EF, GH đồng quy
Thảo luận (1)Hướng dẫn giải
Bài 85* (Sách bài tập - trang 90)
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy.
Chứng minh rằng :
\(AA'=BB'+DD'\)
Thảo luận (1)Hướng dẫn giải
