Giải các phương trình sau:
a) \(\left( {{x^2} - 4} \right) + x\left( {x - 2} \right) = 0;\)
b) \({\left( {2x + 1} \right)^2} - 9{x^2} = 0.\)
Giải các phương trình sau:
a) \(\left( {{x^2} - 4} \right) + x\left( {x - 2} \right) = 0;\)
b) \({\left( {2x + 1} \right)^2} - 9{x^2} = 0.\)
Giải các phương trình sau:
a) \(\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};\)
b) \(\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.\)
Thảo luận (1)Hướng dẫn giảia) \(\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};\)
ĐKXĐ: \(x \ne - 1;x \ne \frac{{ - 1}}{2}.\)
Quy đồng mẫu thức ta được:
\(\frac{{2\left( {x + 1} \right)}}{{\left( {2x + 1} \right)\left( {x + 1} \right)}} + \frac{{1.\left( {2x + 1} \right)}}{{\left( {x + 1} \right)\left( {2x + 1} \right)}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};\)
Khử mẫu ta được:
\(\begin{array}{l}2\left( {x + 1} \right) + 1.\left( {2x + 1} \right) = 3\\4x + 3 = 3\\x = 0\left( {t/m} \right).\end{array}\)
Vậy nghiệm của phương trình đã cho là \(x = 0.\)
b) \(\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.\)
ĐKXĐ: \(x \ne - 1;x \ne \frac{{ - 1}}{2}.\)
Quy đồng mẫu thức ta được: \(\frac{{1.\left( {{x^2} - x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \frac{{x\left( {x + 1} \right)}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}} = \frac{{3x}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}}.\)
Khử mẫu ta được:
\(\begin{array}{l}1.\left( {{x^2} - x + 1} \right) - x\left( {x + 1} \right) = 3x\\ - 2x + 1 = 3x\\5x = 1\\x = \frac{1}{5}\left( {t/m} \right).\end{array}\)
Vậy nghiệm của phương trình đã cho là \(x = \frac{1}{5}.\)
(Trả lời bởi Hà Quang Minh)
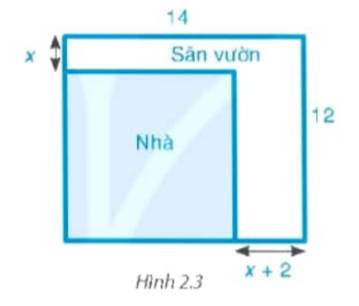
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là \(100{m^2}.\) Hỏi x bằng bao nhiêu mét?
Thảo luận (1)Hướng dẫn giảia) \(x\left( {x - 2} \right) = 0;\)
\(\begin{array}{l}TH1:x = 0\\TH2:x - 2 = 0\\x = 2\end{array}\)
Vậy \(x \in \left\{ {0;2} \right\}.\)
b) \(\left( {2x + 1} \right)\left( {3x - 2} \right) = 0.\)
\(\begin{array}{l}TH1:2x + 1 = 0\\x = \frac{{ - 1}}{2}\\TH2:3x - 2 = 0\\x = \frac{2}{3}\end{array}\)
Vậy \(x \in \left\{ {\frac{{ - 1}}{2};\frac{2}{3}} \right\}.\)
(Trả lời bởi Hà Quang Minh)
Hai người cùng làm chung một công việc thì xong trong 8 giờ. Hai người cùng làm được 4 giờ thì người thứ nhất bị điều đi làm công việc khác. Người thứ hai tiếp tục làm việc trong 12 giờ nữa thì xong công việc. Gọi x là thời gian người thứ nhất làm một mình xong công việc (đơn vị tính là giờ, \(x > 0\)).
a) Hãy biểu thị theo x:
- Khối lượng công việc mà người thứ nhất làm được trong 1 giờ;
- Khối lượng công việc mà người thứ hai làm được trong 1 giờ;
b) Hãy lập phương trình theo x và giải phương trình đó. Sau đó cho biết, nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc đó.
Thảo luận (1)Hướng dẫn giảia)
- Một giờ người thứ nhất làm được số công việc là \(\frac{1}{x}\) (công việc)
- Hai người làm công việc 8 giờ thì xong nên một giờ hai người làm được số công việc là \(\frac{1}{8}\) (công việc)
Nên một giờ người thứ hai làm được \(\frac{1}{8} - \frac{1}{x}\) (công việc)
b) Hai người cùng làm trong 4 giờ thì làm được \(4.\frac{1}{8} = \frac{1}{2}\) (công việc)
Người thứ hai làm tiếp tục một mình trong 12h làm được \(12.\left( {\frac{1}{8} - \frac{1}{x}} \right) = \frac{3}{2} - \frac{{12}}{x}\) (công việc) thì xong công việc nên ta có phương trình:
\(\frac{1}{2} + \left( {\frac{3}{2} - \frac{{12}}{x}} \right) = 1\) hay \(\frac{3}{2} - \frac{{12}}{x} = \frac{1}{2}\) suy ra \(\frac{{12}}{x} = 1\) nên \(x = 12\left( {t/m} \right)\)
Với \(x = 12\) thì một giờ người thứ hai làm được \(\frac{1}{8} - \frac{1}{{12}} = \frac{1}{{24}}\) (công việc)
Do đó thời gian hoàn thành công việc của người thứ hai nếu làm một mình là \(1:\frac{1}{{24}} = 24\) (giờ)
Vậy nếu làm riêng người thứ nhất hoàn thành công việc trong 12 h.
Người thứ hai hoàn thành công việc trong 24h.
(Trả lời bởi Hà Quang Minh)